سلام سایت  www.3RF2008.com  افتتاح شد

نظریه مجموعه ها یک نظریه ریاضی است که در مورد مجموعه ها بحث میکندو مجموعه ای از موضوعات مجرد را ارائه میکندو دارای یک نقش مرکزی در نظریه ریاضیات مدرن است.این نظریه همانند سایر نظریه های ریاضی دارای یک ساختار داخلی توانمند است. روشهای موجود در آن به عنوان یک وسیله قدرتمند در بسیاری از شاخه های ریاضی، کاربردهای فراوانی دارد.
برای آشنایی بیشتر با این نظریه سرفصلهای زیر را ببینید:

• مجموعه:

ما را با مفاهیم مقدماتی نظریه مجموعه ها آشنا میکند.

• naive set theory__:

اصلی ترین قسمت نظریه مجموعه ها که توسط دانشمندان قرن نوزدهم توسعه یافت.

• نظریه مجموعه های بدیهی:

یک نظریه قویتر که برای پاسخگویی به بعضی خدشه های وارد برnaive set theory (مانندآنچه در پارادوکس راسل مطرح شد) ابداع شد.

پارادوکس

پارادوکس

• زمینه تاریخی پارادوکس
• پارادوکس درریاضی

زمینه تاریخی پارادوکس

پیدایش پارادوکس ها زمینه تاریخی دارد.برای فهم بهثر ان داستان زیر را ذکر میکنیم:
در یک روز جمعه دادگاه شخصی را به مرگ محکوم کرد. قاضی به زندانیِ محکوم گفت:

ظهریکی از روزهای هفته‌ی آینده حکم اعدام درباره‌ی تو اجرا خواهد شد، ولی ما آنروز را برای تو مشخص نخواهیم کرد و تو هرگز قبل از آن روز اطلاع پیدا نخواهی کرد و فقط شش ساعت قبل یعنی صبحِ روز اجرای حکم موضوع را به تو اطلاع خواهیم داد.

قاضیِ مذکور در همه‌ی عالم به ذکاوت و خوش‌قولی مشهور بود و همیشه دقیقاً به گفته‌ی خود عمل می‌نمود.

زندانی به همراهی وکیل مدافع خود به سلولش داخل شد و هر دو غمزده در گوشه‌ای به فکر فرو رفتند. ناگاه وکیل مدافع با لبخندی پیروزمندانه سکوت را شکست و گفت:

اجرای حکم قاضی امکان ندارد.

زندانی گفت:

من که چیزی سردر نمی‌آورم. چرا؟

وکیل مدافع پاسخ داد:

اجازه بده تا درست برایت شرح دهم: مسلماًً آن‌ها روز جمعه نمی‌نتوانند تو را اعدام کنند. به دلیلِ اینکه اگر فرضاً بخواهند در روز جمعه‌ی آینده حکم را اجرا نمایند. در این صورت تو تمام روزهای هفته و همچنین بعدازظهر پنج‌شنبه زنده خواهی بود و چون فقط روز جمعه یعنی یک روز دیگر به مهلت باقی مانده، بعد ازظهر پنج‌شنبه برای تو مسلم خواهد شد که فردا یعنی روز جمعه و تنها روز آخر هفته ، حکم اجرا خواهد شد. در نتیجه تو روز اجرای حکم را یک روز پیش‌تر پیش‌بینی و قبل از صبح جمعه از آن اطلاع حاصل کرده‌ای و این موضوع نقض حکم قاضی بوده و گفته‌ی او را بی‌اعتبار خواهد کرد.


زندانی گفته‌ی او را تصدیق کرد.وکیل مدافع ادامه داد:

بنابراین روز جمعه‌ی آینده از فهرستِ روزهای مهلت حذف و در آن روز حکم غیرقابل اجرا است. و اما روز پنج‌شنبه نیز نمی‌توانند تو را اعدام کنند چون در بعدازظهرِ چهارشنبه دو روز بیشتر به آخر هفته نمانده و چون روز جمعه از فهرست حذف شد ، تنها روز پنج‌شنبه آخرین روز اجرای حکم می‌باشد نتیجتاً بعدازظهر چهارشنبه تو خواهی دانست در روز پنج‌شنبه که آخرین روز امکان اجرای حکم است، تو را اعدام خواهند کرد. اطلاع تو یک روز پیشتر از اجرای حکم مجدداً متناقض با حکم قاضی است. بنابراین پنج‌شنبه نیز حکم غیرقابل اجرا است. چهارشنبه نیز امکان اجرای حکم وجود ندارد چون جمعه و پنج‌شنبه حکم غیرقابل اجرا شد و فقط چهارشنبه آخرین روز اجرای حکم تشخیص داده شد و تو که بعدازظهر سه‌شنبه هنوز زنده هستی، اجرای حکم روز چهارشنبه را پیش‌بینی خواهی کرد و از آن اطلاع خواهی یافت.

در این موقع که زندانی از حالت غمزدگی بیرون آمده بود با لبخندی مسرت‌بخش گفت:

پس به هر طریق می‌توان گفت که روز سه‌شنبه و سپس دوشنبه و بالاخره یک‌شنبه نمی‌توانند مرا اعدام کنند و فقط فردا یعنی شنبه باقی است. و اما فردا نیز اجرای حکم برای آنها غیرممکن است چون در این صورت من امروز موضوع را خواهم فهمید.


ملاحظه می‌شود از لحاظ منطقی هیچ تناقضی در حکم قاضی جهت اعدام زندانی وجود ندارد با این وجود حکمش غیرقابل اجرا است. به دلایل بالا به نظر می‌آید که حکم قاضی باعث نقض حکم خودش شده است، اگر حکم را اجرا کند خلاف حکم خودش شده است، اگر حکم را اجرا کند خلاف حکم خود عمل کرده و اگر اجرا نکند باز هم خلاف حکم خود رفتار نموده.


روایت دیگری از این پارادکس از یک اعلامیه‌ی فرمانده‌ی نظامی گفتگو می‌کند که در آن ذکر شده:

برای تمرین ، در یکی از شبهای هفته‌ی آینده آژیر خطر کشیده خواهد شد. شب تمرین در شش بعدازظهر همان روز به اطلاع عامه خواهد رسید و تا شش بعدازظهر کسی از شب موعود مطلع نخواهد شد.


به ظاهر چنین به نظر می رسد که خود این اعلامیه ثابت می‌کند که تمرین هرگز انجام نخواهد گرفت. به زبان دیگر اجرای تمرین عملی نیست مگر این که به متن اعلامیه عمل نشود.

پارادوکس درریاضی

در ریاضیات نیز میتوان به یک پارادوکس مهم در نظریه مجموعه ها به نام پارادوکس راسل اشاره کرد:
مجموعهA را مجموعه ای تعریف می کنیم که شامل اعضای خود نباشد .یعنی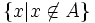

در این صورت اگر 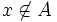انگاه

اگر 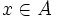انگاه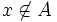

که این پارادوکس از معروفثرین پارادوکس ها در نظریه مجموعه هامی باشد

منطق فازی

ریاضیات فازی یک فرا مجموعه از منطق بولی است که بر مفهوم درستی نسبی، دلالت می کند. منطق کلاسیک هر چیزی را بر اساس یک سیستم دوتائی نشان می دهد ( درست یا غلط، 0 یا 1، سیاه یا سفید) ولی منطق فازی درستی هر چیزی را با یک عدد که مقدار آن بین صفر و یک است نشان می دهد. مثلاً اگر رنگ سیاه را عدد صفر و رنگ سفید را عدد 1 نشان دهیم، آن گاه رنگ خاکستری عددی نزدیک به صفر خواهد بود. در سال 1965، دکتر لطفی‌زاده نظریه سیستم‌های فازی را معرفی کرد. در فضایی که دانشمندان علوم مهندسی به دنبال روش‌های ریاضی برای شکست دادن مسایل دشوارتر بودند، نظریه فازی به گونه‌ای دیگر از مدل‌سازی، اقدام کرد.

منطق فازی معتقد است که ابهام در ماهیت علم است. بر خلاف دیگران که معتقدند که باید تقریب‌ها را دقیق‌تر کرد تا بهره‌وری افزایش یابد، لطفی‌زاده معتقد است که باید به دنبال ساختن مدل‌هایی بود که ابهام را به عنوان بخشی از سیستم مدل کند. در منطق ارسطویی، یک دسته‌بندی درست و نادرست وجود دارد. تمام گزاره‌ها درست یا نادرست هستند. بنابراین جمله «هوا سرد است»، در مدل ارسطویی اساساً یک گزاره نمی‌باشد، چرا که مقدار سرد بودن برای افراد مختلف متفاوت است و این جمله اساساً همیشه درست یا همیشه نادرست نیست. در منطق فازی، جملاتی هستند که مقداری درست و مقداری نادرست هستند. برای مثال، جمله "هوا سرد است" یک گزاره منطقی فازی می‌باشد که درستی آن گاهی کم و گاهی زیاد است. گاهی همیشه درست و گاهی همیشه نادرست و گاهی تا حدودی درست است. منطق فازی می‌تواند پایه‌ریز بنیانی برای فن‌آوری جدیدی باشد که تا کنون هم دست‌آورد‌های فراوانی داشته است.

از منطق فازی برای ساخت کنترل کننده های لوازم خانگی از قبیل ماشین رختشویی (برای تشخیص حداکثر ظرفیت ماشین، مقدار مواد شوینده، تنظیم چرخهای شوینده) و یخچال استفاده می شود. کاربرد اساسی آن تشخیص حوزه متغیرهای پیوسته است. برای مثال یک وسیله اندازه گیری دما برای جلوگیری از قفل شدن یک عایق ممکن است چندین عضو مجزا تابعی داشته باشد تا بتواند حوزه دماهایی را که نیاز به کنترل دارد به طور صحیح تعریف نماید. هر تابع، یک ارزش دمایی مشابه که حوزه آن بین 0 و 1 است را اختیار می کند. از این ارزشهای داده شده برای تعیین چگونگی کنترل یک عایق استفاده می شود.

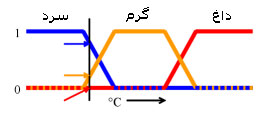در شکل روبرو، سرد بودن، گرم بودن و داغ بودن، توابعی برای مقایسه درجه حرارت هستند و هر نقطه ای روی این خطوط می تواند دارای یکی از سه ارزش بالا باشد. به عنوان مثال برای یک درجه حرارت خاص که در شکل با یک خط نشان داده شده است، می توان گفت: «مقداری سرد است»،«اندکی گرم است» یا «اصلاً داغ نیست».
حال با مثال دیگری اهمیت این علم را بیشتر درک مینمائیم:
یک انسان در نور کافی قادر به درک میلیونها رنگ میباشد.ولی یک روبوت چگونه میتواند این تعداد رنگ را تشخیص دهد؟ حال اگر بخواهیم روباتی طراحی کنیم که قادر به تشخیص رنگها باشد از منطق فازی کمک میگیریم و با اختصاص اعدادی به هر رنگ آن را برای روبوت طراحی شده تعریف میکنیم.
از کاربردهای دیگر منطق فازی میتوان به کاربرد این علم در صنعت اتومبیل سازی(در طراحی سیستم ترمز ABS و کنترل موتور برای بدست آوردن بالاترین راندمان قدرت)،در طراحی بعضی از ریزپردازنده ها و طراحی دوربینهای دیجیتال اشاره کرد.