سلام سایت www.3RF2008.com افتتاح شدبزرگترین مقسوم علیه مشترک |
تعریف:
مقسوم علیه های مشترک میان دو عددa وb، اعدادی هستند که بتوانند هم a و هم b را بشمارند به عبارت ریاضی: اگر c مقسوم علیه مشترک دو عدد a و b باشد، آنگاه c|a و c|b .
مثلا مقسوم علیه های دو عدد 15 و30 را داریم:
{15={1,3,5,15}
30={1,2,3,5,6,10,15,30}
مقسوم علیه های مشترک میان این دو عدد عبارتند از:
مقسوم علیه های مشترک:{1,3,5,15}
بزرگترین مقسوم علیه مشترک میان دو عدد، عددی است که نسبت به تمام مقسوم علیه های مشترک میان دو عدد، بزرگترین باشد. به عبارت ریاضی: اگر d بزرگترین مقسوم علیه باشد، d|a و d|b و dبزرگتر از c باشد.
بزرگترین مقسوم علیه مشترک میان این دو عدد ، 15 است. که آن را به این صورت نمایش می دهند:
(15,30)=15
بزرگترین مقسوم علیه میان دو عدد را به اختصار به صورت " ب.م.م " می نویسند.
اگر ب.م.م دو عدد یک باشند ، آنگاه این دو عدد نسبت به هم اولند.مثلا دو عدد 13 و 8 هیچ مقسوم علیه مشترکی جز یک ندارند.
قضایای مربوط به بزرگترین مقسوم علیه مشترک:
قضیه1) این قضیه به قضیه بزو نیز معروف است. مطابق این قضیه مجموعه زیر مجموعه ای از مقسوم علیه های مشترک میان دو عدد a وb هستند:S={m,n ? Z| am+bn>0}
نتیجه ای که از این قضیه می توان گرفت آن است که بزرگترین مقسوم علیه مشترک میان دو عدد aو b مطابق فرمول زیر است:
Am+bn=d.
قضیه 2) d بزرگترین مقسوم علیه مشترک دو عدد a و b است اگر و فقط اگر :
الف) d|a و d|b و ب) اگر c|a و c|b آنگاه c|d.
قضیه 3) اگر a|bc و (a,b)=1 یعنی نسبت به هم اول باشند، آنگاه a|c . این قضیه به لِم اقلیدوس نیز معروف است.
قضیه4) اگر P|ab (P یک عدد اول است)، آنگاه P|a یا P|b .
قضیه5) اگر c کوچکترین مضرب مشترک و d بزرگترین مقسوم علیه مشترک دو عدد a وb باشد آنگاه داریم:
Then: d*c=ab
لم های مربوط به بزرگترین مقسوم علیه های مشترک:
لم 1) بر اساس اصول بنیادی حساب، هر عدد مرکب را می توان به صورت حاصلضرب اعداد اول تجزیه کرد. ب.م.م میان دو عدد برابر با حاصلضرب اعداد اول مشترک میان آن دو عدد به توان عدد کمتر.لم 2) ب.م.م دو عدد، هر مقسوم علیه مشترک میان دو عدد را می شمارد:
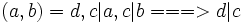
لم 3) اگر
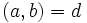 آنگاه :
آنگاه : 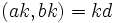
لم 4) اگر
a|c & b|c , (a,b)=1 ===> ab|c
لم 5) اگر
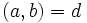 آنگاه
آنگاه 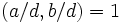
مثال مربوط به بزرگترین مقسوم علیه مشترک :
مثال1) اگر n عددی فرد باشد ثابت کنید که 24حاصلضرب سه عدد متوالی قبل و بعد از n را می شمرد:
24|(n-1)n(n+1)
جواب:
عدد سه، حاصلضرب سه عدد متوالی را می شمرد( اثبات آن به عهده خواننده است. راهنمایی : هر عددی را می توان به صورت :
A=3q+r 0?r<3) 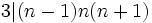
باید ثابت کنیم که حاصلضرب دو عدد زوج متوالی بر 8 تقسیمپذیر است: 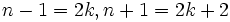 :
:
then: 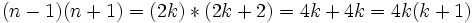
حاصلضرب دو عدد متوالی همواره بر 2 بخش پزیر است.پس: 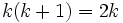
then: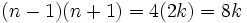
then: 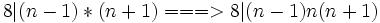
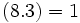 then:
then:
طبق لم 4 داریم: 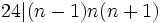
اعداد اول
تعریف:عدد طبیعی p>1,pرا اول می نامند به شرطی که تنها مقسوم علیه های مثبت آن 1وp باشند. اگرعددی طبیعی وبزرگتر از 1اول نباشد مرکب است.
قضیه 1: تعداد اعداد اول نامتناهی است.
برهان: حکم را به روشی که منسوب به اقلیدس است اثبات می کنیم: فرض کنید تعداد اعداد اول متناهی و تعداد آنها n تا باشد . حال عدد M را که برابر حاصلضرب این اعداد به علاوه ی 1 را در نظر بگیرید. این عدد مقسوم علیهی غیر از آن n عدد دارد که با فرض در تناقض است.
(البته شایان ذکر است که این قضیه اثبات های گوناگونی دارد که ما ساده ترین آنها را انتخاب کردیم اگر مایلید می توانید اثبات های دیگر آن را بیاورید.)
قضیه 2:قضیه ی اساسی حساب: هر عدد طبیعی بزرگتر از 1 را به شکل حاصلضرب اعدادی اول نوشت.
قضیه 3: قضیه چپیشف:اگر n عددی طبیعی و بزرگتر از 2 باشد, حتما" بین n و 2n عدد اولی وجود دارد. (شخصا" توصیه میکنم از اثبات کردن این قضیه خودداری کنید)
همنهشتی |
تعریف:
اگر m یک عدد طبیعی و a وb دو عدد صحیح باشند، و m بتواند اختلاف بین aوb را بشمارد، آنگاه می گوییم a همنهشت با a است به پیمانه m.
رابطه همنهشتی یک رایطه هم ارزی است پس این رابطه می تواند مجموعه Z را افراز کند. به مثال 2 در این زمینه توجه کنید.
ویژگی های همنهشتی:
- اگر b?a به پیمانه m آنگاه داریم:
A+c?b+c و بلعکس
- اگر
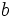 و
و 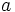 باهم همنهشت و
باهم همنهشت و 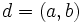 و
و  به همنهشت به پیمانه m آنگاه داریم:
به همنهشت به پیمانه m آنگاه داریم:
ac?bc به پیمانه m
- اگر b?a به پیمانه m داشته باشیم آنگاه به ازای n های طبیعی داریم:
 و
و  با هم همنهشتند به پیمانه m
با هم همنهشتند به پیمانه m
- اگر به ازای تمام aوb های همنهشت به پیمانه m داشته باشیم،آنگاه مجموع و حاصلضرب متناظرشان نیز باهم همتهشتند به پیمانه m.
- اگر b?a به پیمانه m داشته باشیم و c عدد صحیحی باشد، آنگاه داریم:
ac?bc به پیمانه m.
قضایای مربوط به همنهشتی:
قضیه 1) اگر ac?bc به پیمانه m و آنگاه داریم:
آنگاه داریم:
a?b به پیمانه m/d
لم مربوط به همنهشتی:
لم1) اگر a?b به پیمانه m باشد و d یکی ازمقسوم علیه های m باشد آنگاه داریم:
a?b به پیمانه d
لم2) اگر  و
و  باهم همنهشت به پیمانه m و
باهم همنهشت به پیمانه m و آنگاه داریم:
آنگاه داریم:
a?b به پیمانه m
لم 3) اگر r باقیمانده تقسیم a بر m باشد، انگاه، a?r به پیمانه m.
مثال مربوط به همنهشتی:
مثال1) 36همنهشت با18 به پیمانه 6. یعنی 36-18=18 و 18|6 و به عبارتی دیگر،8 بر 6 بخش پذیر است.
مثال2) مجموعه اعدادی را بیابید که اختلافشان بر عدد 2 بخش پذیر باشد.
جواب:
تمام اعداد صحیح بخش پذیر بر 2 عبارتند از:
A=2q+r 0?r<2
پس داریم:
A=2q and a=2q+1
{  به طوری که اختلاف این اعداد با عدد 2، همواره بر 2 بخش پذیر است. یعنی می توان گفت x1?x2 به پیمانه 2.
به طوری که اختلاف این اعداد با عدد 2، همواره بر 2 بخش پذیر است. یعنی می توان گفت x1?x2 به پیمانه 2.
و همچنین داریم:
{  }
}
به طوری که اختلاف این اعداد با عدد 2، همواره بر 2 بخش پذیر است. یعنی می توان گفت z1?z2 به پیمانه 2.
اعداد اول |
تعریف:عدد طبیعی p>1,pرا اول می نامند به شرطی که تنها مقسوم علیه های مثبت آن 1وp باشند. اگرعددی طبیعی وبزرگتر از 1اول نباشد مرکب است.
قضیه 1: تعداد اعداد اول نامتناهی است.
برهان: حکم را به روشی که منسوب به اقلیدس است اثبات می کنیم: فرض کنید تعداد اعداد اول متناهی و تعداد آنها n تا باشد . حال عدد M را که برابر حاصلضرب این اعداد به علاوه ی 1 را در نظر بگیرید. این عدد مقسوم علیهی غیر از آن n عدد دارد که با فرض در تناقض است.
(البته شایان ذکر است که این قضیه اثبات های گوناگونی دارد که ما ساده ترین آنها را انتخاب کردیم اگر مایلید می توانید اثبات های دیگر آن را بیاورید.)
قضیه 2:قضیه ی اساسی حساب: هر عدد طبیعی بزرگتر از 1 را به شکل حاصلضرب اعدادی اول نوشت.
قضیه 3: قضیه چپیشف:اگر n عددی طبیعی و بزرگتر از 2 باشد, حتما" بین n و 2n عدد اولی وجود دارد. (شخصا" توصیه میکنم از اثبات کردن این قضیه خودداری کنید)
تئوری اعداد
تئوری اعداد number theory شاخه ای از ریاضیات محض pure mathematics است که در مورد خواص اعداد صحیح integers بحث می کند و حاوی بسیاری مسائل است که حتی غیر ریاضیدانان به راحتی آنها را متوجه می شوند .به طور کلی ایـن شاخه ، مسائل مربوط به مطالعه اعداد صحیح را مطرح می کند. تئوری اعداد را می توان بنا به روشهای بررسی سؤالات به چندین بخش تقسیم کرد. مثلاً به سرفصل های تئوری اعداد مراجعه نمایید .

-
تئوری مقدماتی اعداد ،اعداد صحیح را بدون توجه به تکنیک های ریاضی به کار رفته در سایر شاخه ها بررسی می کند . مسائل بخشپذیری divisibility ، الگوریتم اقلیدسیEuclidean algorithm ، محاسبه ی بزرگترین مقسوم الیه مشترک greatest common divisors ، تجزیه ی اعداد به اعداد اول prime numbers ، جستجوی عدد تام perfect number و همنهشتی ها congruences در این رده هستند . نمونه ها قضیه ی کوچک فرما Fermat’s little theorem ، و قضیه ی اولر Euler’s theoremهستند و به طور عام قضیه ی باقیمانده ی چینی Chinese remainder theorem و قانون تقابل درجه ی دوم quadratic reciprocity هستند . خواص توابع ضربیmultiplicative functions مانند تابع موبیوس Mobius function و تابع اولر Euler"s ? function و همینطور دنباله ی اعداد صحیح integer sequences مانند فاکتوریل هاfactorials و اعداد فیبوناچی Fibonacci numbers در همین حوزه بررسی میشوند . بسیاری از سؤالات در تئوری مقدماتی اعداد شدیداً عمیق هستند و نیاز به بازنگری هایی دارند . به عنوان نمونه :
-
انگارهی گلدباخ Goldbach conjecture که میگوید آیا هر عدد زوجی حاصلجمع دو عدد اول است یا نه.
-
انگارهی کاتالان Catalan’s conjecture که در مورد توانهای متوالی اعداد صحیح است .
-
انگارهی اعداد اول دوقلو Twin prime conjecture که در مورد بینهایت بودن اعداد اول دوقلو است.
-
انگارهی کولاتز Collatz conjecture که در مورد تکرار ساده میباشد .
-
معادلات دیوفانتیDiophantine نیز هنوز تصمیم ناپذیر است.
-
تئوری تحلیلی اعداد Analytic number theory ازحسابانcalculus و آنالیز مختلطcomplex analysis برای مطالعهی اعداد صحیح استفاه می کند و با سؤالاتی در مورد اعداد صحیح دست و پنجه نرم می کند که در تئوری مقدماتی اعداد بررسی و بحث در مورد آن بسیار دشوار به نظر میرسد . قضیه ی اعداد اولprime number theorem و فرضیه ریمان Riemann hypothesis مثال هایی از آن هستند . مسئله ی وارینگ Waring’s problem ( که عدد صحیحی را به صورت جمع چند مربع یا مکعب چند عدد نشان می دهد ) ،انگارهی اعداد اول دوقلو Twin prime conjecture(که تعداد بینهایت عدد اول با اختلاف 2 را پیدا می کند ) ، و فرضیه ی گلدباخGoldbach’s conjecture ( که عددهای زوج داده شده را به صورت مجموع دو عدد اول پیدا می کند ) با روشهای تحلیلی مورد حمله قرار گرفته شده اند . اثبات متعالی بودن transcendence ثابت های ریاضی ، مانند e و پی در بخش تئوری اعداد تحلیلی قرار دارند . بعضی ها حکم هایی در مورد اعداد متعالی را از محدوده ی مطالعات اعداد صحیح خارج می کنند ، در واقع مقادیر ممکن برای چند جمله ایها با ضریب های صحیح مانند e و پی به مبحث تقریب دیوفانتین Diophantine aproximation ارتباط نزدیک دارند ؛ و سؤال آنها این است که چگونه می توان یک عدد حقیقی داده شده را با یک عدد گویا rational تقریب زد ؟
-
تئوری جبری اعداد ، مفهوم عدد را به اعداد جبری algebraic numbers که همان ریشه های چند جمله ایها با ضرایب گویا rational coefficient هستند گسترش میدهد.در این حوزه مباحثی همانند اعداد صحیح به نام اعداد صحیح جبری algebraic integers وجود دارد . در اینجا لازم نیست به صورت های آشنای اعداد صحیح ، ( مانند تجزیه یکتا the unique factorization) پایبند باشیم .مزیت روش استفاده شده --تئوری گالوا Galois theory ، میدان همانستگی field cohomology ، تئوری رده ی میدان class field theory ، نمایش گروه ها group representations و L-تابعها L-functions این است که به ما اجازه می دهدبرای این رده از اعداد ، این ترتیب را تا حدودی بپوشانیم .تعدادی از سؤالات قضیه ی اعداد با مطالعه پیمانه p برای کلیه اعداد اول p مورد حمله قرار گرفته شده اند . (به میدانهای متناهی finite fields مراحعه کنید ) .به چنین چیزی localization می گویند که به ساختمان اعداد p ادیک p-adic numbers می انجامد . به این محدوده تحلیل موضعی local analysis می گویند که از تئوری اعداد جبری ناشی می شود .
-
تئوری ترکیبیاتی اعداد به بررسی ، مطالعه و حل مسالههای تئوری اعداد با استفاده از تکنیکهای ترکیبیاتی میپردازد. پل اردوش کارهای بزرگی در این زمینه انجام داد. روشهای جبری و تحلیلی در این شاخه از تئوری اعداد کاربرد فراوان دارند.
-
تئوری هندسی اعداد همه ی فرم های هندسی را در بر می گیرد ؛و از قضیه ی مینکوسکی Minkowski’s theorem در ارتباط با نقاط مشبکه lattice points در مجموعه های محدب convex sets و جستجو در بسته بندی کره ها sphere packings شروع می شود .هندسه جبری بخصوص خمهای بیضویelliptic curves نیز به کار می آیند .این تکنیکها در اثبات آخرین قضیه معروف فرما Fermat’s last theorem تاثیر فراوان داشته اند .
-
تئوری محاسباتی اعداد computational number theory به الگوریتم های تئوری اعداد می پردازد والگوریتم های سریع برای امتحان اعداد اول prime testing و تجزیه اعداد صحیح integer factorization در مبحث کریپتوگرافی cryptography کاربرد های مهمی دارند .
.
 |
تاریخچه تئوری اعداد
چبیشفChebyshev کران هایی برای تعداد اعداد اول بین یک بازه ارائه داد . ریمان Riemann اظهار کرد که حد تعداد اعداد اول از یک عدد داده شده تجاوز نمی کند . (قضیه ی عدد اول prime number theory. ) و آنالیز مختلط complex analysis را در تئوری تابع زتای ریمان Riemann zeta function گنجاند و فرمول صریح تئوری اعداد اول explicit formulae of prime number theory را از صفر های آن نتیجه گرفت .
تئوری همنهشتی congruences از Disquisitiones گاوس شروع شد . او علامت گذاری زیر را پیشنهاد کرد :
چبیشف در سال 1847 به زبان روسی کاری را در این زمینه منتشر کرد و سره Serret آن را در فرانسه عمومی کرد . بجای خلاصه کردن کارهای قبلی ، لوژاندر قانون تقابل درجه ی دوم law of quadratic reciprocity را گذاشت . این قانون از استقراء induction کشف شد و قبلاً اولر آن را مطرح کرده بود. لوژاندر در تئوری اعداد Théorie des Nombres برای حالت های خاص آن را ثابت کرد . جدا از کارهای اولر و لوژاندر ، گاوس این قانون را در سال 1795 کشف کرد و اولین کسی بود که یک اثبات کلی ارائه داد . کوشی Cauchy ؛ دیریکله Dirichlet ( که مقاله ی Vorlesungen über Zahlentheorie او یک مقاله ی کلاسیک است) ؛ ژاکوبی Jacobi که علامت ژاکوبی Jacobi symbol را معرفی کرد ؛ لیوویلLiouville ؛ زلرZeller ؛ آیزنشتین Eisenstein؛ کومرKummer و کرونکر Kronecker نیز در این زمینه کارهایی کرده اند . این تئوری تقابل درجه دوم و سوم cubic and biquadratic reciprocity را شامل می شود. نمایش اعداد با صورت درجه ی دوم دوتایی binary quadratic forms مدیون گاوس است . کوشی ، پوانسو Poinsot ، لبگ Lebesgue و بخصوص هرمیت Hermite به موضوع چیزهایی افزوده اند . آیزنشتاین Eisenstein در تئوری صورت های سه گانه پیشتاز است ، و تئوری فرمها theory of forms به طور کلی مدیون او و اچ. اسمیتH. J. S. Smith است. اسمیت دسته بندی کاملی از صورتهای سه گانه انجام داد و تحقیقات گاوس در مورد صورت های درجه ی دوم حقیقی به فرمهای مختلط افزود . جستجوهایی در مورد نمایش اعداد به صورت جمع 4، 5 ،6 ، 7 ، 8 ، مربع توسط آیزنشتاین ادامه یافت و اسمیت آن را کامل کرد .
[ شنبه 87/2/7 ] [ 4:34 عصر ] [ مهندسی مکانیک(امین احمدی) ]

