سلام سایت www.3RF2008.com افتتاح شد
مطالعه روی زوایا و روابط موجود میان زوایااشکال مسطح و سه بعدی مثلثات نامیده میشود.توابع مثلثاتی از قبیل سینوس و کسینوس توابعی هستند که بوسیله روابط هندسی تعریف میشوند.
تاریخچه
اولین کسانی که از مثلثات استفاده میکردند یونانیان بودند.در یونان قدیم از مثلثات برای تعیین طول مدت روز یا طول سال (با مشخص کردن موقعیت ستارگان در آسمان)استفاده میشد.بعدها ریاضیدانان و منجمان هندی نیز پیشرفتهایی در مثلثات بدست آوردندولی پیشرفت این علم مدیون دانشمندان مسلمان است .مسلمانان اصلی ترین نقش را در پیشرفت این علم ایفا کردند و سپس این اندوخته ها را در قرون وسطی به اروپاییان منتقل کردند.اروپاییان نیز دانش فراوان مسلمانان در مثلثات استفاده کردندو این علم را توسعه داده و به شکل امروزی در آوردند.کاربردها
علم مثلثات در نجوم کاربرد فراوانی دارد و ازآن برای اندازه گیری فواصل بین ستارگان استفاده میشود. همچنین در طراحی سیستم های ماهواره ای از مثلثات استفاده فراوانی میشود.در دریانوردی نیز از مثلثات برای تشخیص جهت های جغرافیایی کمک گرفته میشود.امروزه از مثلثات در شاخه های مختلف فیزیک ماننداپتیک،اکوستیک،در آنالیز بازار مالی،الکترونیک،معماری، اقیانوس شناسی،مکانیک،بلور شناسی،ژئودزی،عمران و اقتصاداستفاده فراوانی میشود.تابع مثلثاتی
مثلثات مطالعه اندازه گیری زاویه است. اما این سخن به معنی اندازه گیری مقدماتی زاویه در هندسه نیست که در آن مقدار زاویه مورد نظر هر یک نقاله خوانده می شود بلکه محاسبه با توابع خاصی است که بستگی به زوایا دارند و به علت کابردشان در مثلثات، توابع مثلثاتی نامیده می شوند.
 |
تعریف روی مثلث قائم الزاویه
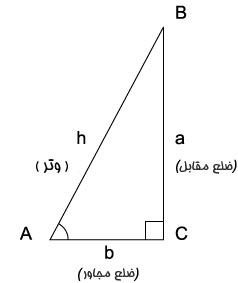
برای تعریف توابع مثلثاتی از یک مثلث قائم الزاویه استفاده می کنیم به عنوان مثال می خواهیم این توابع را برای زاویه A در شکل روبرو تعریف کنیم
ما برای استفاده از این مثلث نامگذاری زیر را انجام می دهیم.
وتر ضلعی است که روبروی زاویه قائم قرار دار که بلندترین ضلع مثلث نیز می باشد و آن را با h نشان داده شده است.
ضلع مقابل زاویه A که آن را با a نشان می دهیم.
ضلع مجاور زاویه قائمه که درشکل با b نشان داده شده است.
حال توابع مثلثاتی را برای زاویه A روی مثلث ABC تعریف می کنیم.
-
sin: نسبت ضلع مقابل به وتر را سینوس می گویند یعنی:
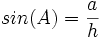
-
cos: نسبت ضلع مجاور به وتر را گویند یعنی داریم:
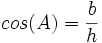
-
tangent: نسبت ضلع مقابل زاویه به ضلع مجاور را گویند.
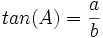
-
cosecant: نسبت وتر به ضلع مقابل زاویه را گویند.
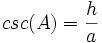
-
secant: نسبت وتر به ضلع مجاور است
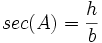
-
cotangent: نسبت ضلع مجاور به ضلع مقابل را گویند.
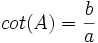
تعریف روی دایره واحد
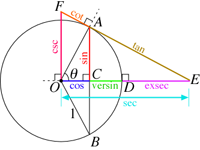 |
در یک صفحه دستگاه مختصات دکارتی، زاویه می تواند هر چهار ربع را طی کند، و مقدار آن می تواند به حسب درجه، گراد رادیان اندازه گیری شود.
ضلع متروک این زاویه، دایره با شعاع و مرکز در مبدا، دایره موسوم به دایره واحد یا یک را در نقطه قطع می کند.
زاویه در تقاطع محور ها با دایره، مقدار صفر را اختیار می کند این زاویه، طی یک دوران کامل ضلع متحرکش حول مبدا از صفحه شروع و پس از رسیدن به مکان اولیه، دارای زاویه 360 درجه می باشد.
روابط مثلثاتی که برای زوایای مختلف برقرار است. برای زوایای بزرگتر از 360 نیز، بر قرار می باشد. مثلا برای دو تابع سینوس و کسینوس خواهیم داشت:
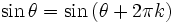
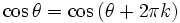
سری فوریه برای بررسی حرکات تناوبی در آکوستیک یا صوت شناسی،الکترودینامیک ،اپتیک یا نور شناسی، ترمودینامیک و غیره مورد استفاده قرار گرفته است.
در مهندسی الکتریک مسائلی چون رفتار بسامدی ،عناصر سوئیچینگ ،یا انتقال ضربه ها را میتوان به کمک سری فوریه حل کرد.
پیش بینی جزرومد در دریانوردی دارای اهمیت فراوانی است.از آنجا که اینها پدیده هایی تناوبی هستند از سری فوریه استفاده میشود و در تمام بندرهای مهم،وسائل مکانیکی چون پیش بینی کننده های جزر و مد ساخته میشود.امروزه کمتر شاخهای از فیزیک،ریاضیات، یا صنعت و فن وجود دارد که در آن از سریهای فوریه استفاده نشود.
تعریف
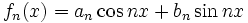
با ضرایب ثابت
 و
و  است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول
است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول  همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی
همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی  ی را نشان میدهد.
ی را نشان میدهد. این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد.
از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن،
 ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب
،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب  و
و  و تابع مجموع
و تابع مجموع  به دست آورد.ضرب سری
به دست آورد.ضرب سری 
در عاملهای کراندار
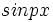 یا
یا 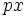 که در آنها p عددی صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان
که در آنها p عددی صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان 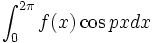 و
و 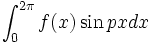
را با استفاده از انتگرالگیری جمله به جمله سری
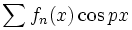 یا
یا 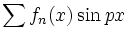 محاسبه کرد
محاسبه کرد این انتگرالگیری ها شامل انتگرال های روی بازه
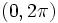 توابع
توابع 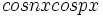 و
و 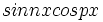 و
و 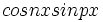 و
و 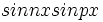 اند.
اند. [ شنبه 87/2/7 ] [ 4:29 عصر ] [ مهندسی مکانیک(امین احمدی) ]

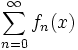 که جمله عمومی آن
که جمله عمومی آن 