[ یکشنبه 87/2/8 ] [ 6:50 عصر ] [ مهندسی مکانیک(امین احمدی) ]
سلام سایت www.3RF2008.com افتتاح شد
آنالیز شاخه ای از ریاضیات است که با اعداد حقیقی و اعداد مختلط و نیز توابع حقیقی و مختلط سر و کار دارد و به بررسی مفاهیمی از قبیل پیوستگی ،انتگرال گیری و مشق پذیری می پردازد
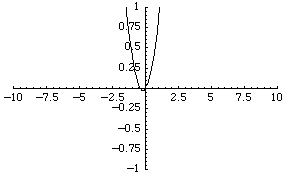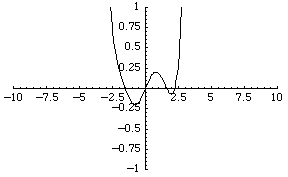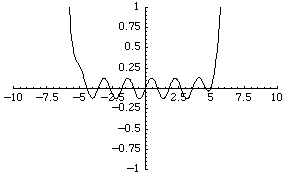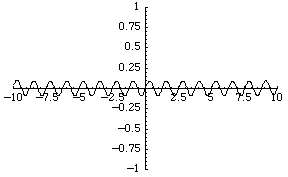 |
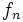 در فضای R که به صفر همگراست در فضای R که به صفر همگراست |
تاریخچه
از نظر تاریخی آنالیز در قرن هفدهم با ابداع حساب دیفرانسیل و انتگرال توسط نیوتن و لایپ نیتس پایه ریزی شد در قرن هفدهم و هجدهم سر فصل های آنالیزی از قبیل حساب تغییرات،معادلات دیفرانسیل با مشتقات جزئی، آنالیز فوریه در زمینه های کاربردی توسعه فراوانی یافتند و از آنها به طور موفقیت آمیز در زمینه های صنعتی استفاده شد. در قرن هجدهم تعریف مفهوم تابع به یک موضوع بحث بر انگیز در ریاضیات تبدیل شد. در قرن نوزدهم کوشی با معرفی مفهوم سری های کوشی اولین کسی بود که حساب دیفرانسیل و انتگرال را بر یک پایه منطقی استوار کرد..در اواسط قرن نوزدهم ریمان تئوری انتگرال گیری خود را که به انتگرال ریمان معروف است ارائه داد در اواخر قرن نوزدهم وایراشتراس مفهوم حد را معرفی کرد و نتایج کار خود بر روی سریها را نیز ارائه داد در همین دوران ریاضیدانان با تلاش های زیاد توانستند انتگرال ریمان را اصلاح نمایند .
در اوایل قرن بیستم هیلبرت برای حل معادلات انتگرال فضای هیلبرتی را تعریف و معرفی نمود.از آخرین تحولات در زمینه آنالیز می توان به پایه گذاری آنالیز تابعی توسط یک دانشمند لهستانی به نام باناچ نام برد.
تقسیم بندی آنالیز
- آنالیز حقیقی: به مطالعه بر روی حد ها ،مشتقات،انتگرال ها سریهای توانی می پردازد.
- آنالیز تابعی: به معرفی نظریه هایی از قبیل فضاهای باناچ و نیز فضای هیلبرت می پردازد.
- آنالیز هارمونیک: در این شاخه از آنالیز سری های فوریه مورد مطالعه قرار می گیرد.
- انالیز مختلط: به بررسی توابع مختلط و خواص این توابع از قبیل مشتق پذیری و انتگرال گیری می پردازد.
آنالیز عددی |
آنالیز عددی الگوریتم حل مسئله در ریاضیات پیوسته(ریاضیاتی که جدا از ریاضیات گسسته است)را مورد مطالعه قرار میدهد. آنالیز عددی اساسا به مسائل مربوط به متغیرهای حقیقی و متغیرهای مختلط و نیز جبر خطی عددی به علاوه حل معادلات دیفرانسیل و دیگر مسائلی که از فیزیک و مهندسی مشتق میشود.
معرفی
تعدادی از مسائل در ریاضیات پیوسته دقیقا با یک الگوریتم حل میشوند.که به روش های مستقیم حل مسئله معروف اند.برای مثال روش حذف گائوسی برای حل دستگاه معادلات خطی است و نیز روش سیمپلکس در برنامه ریزی خطی مورد استفاده قرار میگیرد. ولی روش مستقیم برای حل خیلی از مسائل وجود ندارد.و ممکن است از روشهای دیگر مانند روش تکرارشونده استفاده شود،چون این روش میتواند در یافتن جواب مسئله موثرتر باشد.تخمین زدن خطاها
تخمین خطاهای موجود در حل مسائل از مهمترین قسمت های آنالیز عددی است این خطاها در روش های تکرار شونده وجود دارد چون به هرحال جوابهای تقریبی بدست آمده با جواب دقیق مسئله، اختلاف دارد و یا وقتی که از روش های مستقیم برای حل مسئله استفاده می شود خطاهایی ناشی از گرد کردن اعداد بوجود می آید. در آنالیز عددی می توان مقدار خطا را در خر روش که برای حل مسئله به کار می رود، تخمین زدکاربردها
الگوریتم های موجود در آنالیز عددی برای حل بسیاری از مسائل موجود در علوم پایه و رشته های مهندسی مورد استفاده قرار می گیرند. برای مثال از این الگوریتم ها در طراحی بناهایی مانند پل ها، در طراحی هواپیما ، در پیش بینی آب و هوا، تهیه نقشه های جوی از زمین، تجزیه و تحلیل ساختار مولکول ها، پیدا کردن مخازن نفت، استفاده می شود، همچنین اکثر ابر رایانه ها به طور مداوم بر اساس الگوریتم های آنالیز عددی برنامه ریزی می شوند. به طور کلی آنالیز عددی از نتایج عملی حاصل از اجرای محاسبات برای پیدا کردن روش های جدید برای تجزیه و تحلیل مسائل، استفاده می کند.نرم افزار ها
امروزه بیشتر الگوریتم ها توسط رایانه اجرا می شوند نرم افزارهایی برای اجرای محاسبات ریاضی طراحی شده اند. از مهمترین و کاربردی ترین آنها می توان به نرم افزارهایی زیر اشاره کرد:
Maple یک نرم افزار برای حل مسائل ریاضی است که اولین بار در سال 1981برای انجام مجموعه ای از محاسبات در دانشگاه waterllo طراحی شد. در سال 1988، این نرم افزار توسعه داده شد و به توسط یک کمپانی کانادایی مستقر در دانشگاه به بازار تجاری کامپیوتر عرضه شد.فروش و عرضه این نرم افزار به بازار سود زیادی را نصیب، صاحبان کمپانی کرد.
معرفی
maple یک مفسر، برای زبان برنامه نویسی پویا است، به طور معمول،عبارات جبری و عبارات منطق در حافظه کامپیوتر، ذخیره می شوند و پس از آن بوسیله این نرم افزار پردازش شده و حل میگردند. از این نرم افزار در حل مسایل مختلف ریاضی از قبیل هندسه، حساب و ... استفاده می شود.
نمونه ای از یک برنامه
معادله دیفرانسیل خطی زیر را در نظر بگیرید
 |
کد زیر این معادله را حل میکند:
((dsolve({diff(y(x),x,x)- 3*y(x)= x,y(0)=1,D(y)(0)=2},y(x)
جدیدترین نگارش این نرم افزار نگارش 6 آن میباشد که قابلیت نمایش اعداد تا 100 رقم اعشار و نیز نگهداری 8000 جمله جبری را داراست.
[ شنبه 87/2/7 ] [ 4:39 عصر ] [ مهندسی مکانیک(امین احمدی) ]
سلام سایت www.3RF2008.com افتتاح شد
نظریه مجموعه ها یک نظریه ریاضی است که در مورد مجموعه ها بحث میکندو مجموعه ای از موضوعات مجرد را ارائه میکندو دارای یک نقش مرکزی در نظریه ریاضیات مدرن است.این نظریه همانند سایر نظریه های ریاضی دارای یک ساختار داخلی توانمند است. روشهای موجود در آن به عنوان یک وسیله قدرتمند در بسیاری از شاخه های ریاضی، کاربردهای فراوانی دارد.
برای آشنایی بیشتر با این نظریه سرفصلهای زیر را ببینید:
ما را با مفاهیم مقدماتی نظریه مجموعه ها آشنا میکند.
اصلی ترین قسمت نظریه مجموعه ها که توسط دانشمندان قرن نوزدهم توسعه یافت.
یک نظریه قویتر که برای پاسخگویی به بعضی خدشه های وارد برnaive set theory (مانندآنچه در پارادوکس راسل مطرح شد) ابداع شد.
پارادوکس
پارادوکس
پارادوکس
-
زمینه تاریخی پارادوکس
-
پارادوکس درریاضی
زمینه تاریخی پارادوکس
پیدایش پارادوکس ها زمینه تاریخی دارد.برای فهم بهثر ان داستان زیر را ذکر میکنیم:
در یک روز جمعه دادگاه شخصی را به مرگ محکوم کرد. قاضی به زندانیِ محکوم گفت:
ظهریکی از روزهای هفتهی آینده حکم اعدام دربارهی تو اجرا خواهد شد، ولی ما آنروز را برای تو مشخص نخواهیم کرد و تو هرگز قبل از آن روز اطلاع پیدا نخواهی کرد و فقط شش ساعت قبل یعنی صبحِ روز اجرای حکم موضوع را به تو اطلاع خواهیم داد.
قاضیِ مذکور در همهی عالم به ذکاوت و خوشقولی مشهور بود و همیشه دقیقاً به گفتهی خود عمل مینمود.
زندانی به همراهی وکیل مدافع خود به سلولش داخل شد و هر دو غمزده در گوشهای به فکر فرو رفتند. ناگاه وکیل مدافع با لبخندی پیروزمندانه سکوت را شکست و گفت:
اجرای حکم قاضی امکان ندارد.
زندانی گفت:
من که چیزی سردر نمیآورم. چرا؟
وکیل مدافع پاسخ داد:
اجازه بده تا درست برایت شرح دهم: مسلماًً آنها روز جمعه نمینتوانند تو را اعدام کنند. به دلیلِ اینکه اگر فرضاً بخواهند در روز جمعهی آینده حکم را اجرا نمایند. در این صورت تو تمام روزهای هفته و همچنین بعدازظهر پنجشنبه زنده خواهی بود و چون فقط روز جمعه یعنی یک روز دیگر به مهلت باقی مانده، بعد ازظهر پنجشنبه برای تو مسلم خواهد شد که فردا یعنی روز جمعه و تنها روز آخر هفته ، حکم اجرا خواهد شد. در نتیجه تو روز اجرای حکم را یک روز پیشتر پیشبینی و قبل از صبح جمعه از آن اطلاع حاصل کردهای و این موضوع نقض حکم قاضی بوده و گفتهی او را بیاعتبار خواهد کرد.
زندانی گفتهی او را تصدیق کرد.وکیل مدافع ادامه داد:
بنابراین روز جمعهی آینده از فهرستِ روزهای مهلت حذف و در آن روز حکم غیرقابل اجرا است. و اما روز پنجشنبه نیز نمیتوانند تو را اعدام کنند چون در بعدازظهرِ چهارشنبه دو روز بیشتر به آخر هفته نمانده و چون روز جمعه از فهرست حذف شد ، تنها روز پنجشنبه آخرین روز اجرای حکم میباشد نتیجتاً بعدازظهر چهارشنبه تو خواهی دانست در روز پنجشنبه که آخرین روز امکان اجرای حکم است، تو را اعدام خواهند کرد. اطلاع تو یک روز پیشتر از اجرای حکم مجدداً متناقض با حکم قاضی است. بنابراین پنجشنبه نیز حکم غیرقابل اجرا است. چهارشنبه نیز امکان اجرای حکم وجود ندارد چون جمعه و پنجشنبه حکم غیرقابل اجرا شد و فقط چهارشنبه آخرین روز اجرای حکم تشخیص داده شد و تو که بعدازظهر سهشنبه هنوز زنده هستی، اجرای حکم روز چهارشنبه را پیشبینی خواهی کرد و از آن اطلاع خواهی یافت.
در این موقع که زندانی از حالت غمزدگی بیرون آمده بود با لبخندی مسرتبخش گفت:
پس به هر طریق میتوان گفت که روز سهشنبه و سپس دوشنبه و بالاخره یکشنبه نمیتوانند مرا اعدام کنند و فقط فردا یعنی شنبه باقی است. و اما فردا نیز اجرای حکم برای آنها غیرممکن است چون در این صورت من امروز موضوع را خواهم فهمید.
ملاحظه میشود از لحاظ منطقی هیچ تناقضی در حکم قاضی جهت اعدام زندانی وجود ندارد با این وجود حکمش غیرقابل اجرا است. به دلایل بالا به نظر میآید که حکم قاضی باعث نقض حکم خودش شده است، اگر حکم را اجرا کند خلاف حکم خودش شده است، اگر حکم را اجرا کند خلاف حکم خود عمل کرده و اگر اجرا نکند باز هم خلاف حکم خود رفتار نموده.
روایت دیگری از این پارادکس از یک اعلامیهی فرماندهی نظامی گفتگو میکند که در آن ذکر شده:
برای تمرین ، در یکی از شبهای هفتهی آینده آژیر خطر کشیده خواهد شد. شب تمرین در شش بعدازظهر همان روز به اطلاع عامه خواهد رسید و تا شش بعدازظهر کسی از شب موعود مطلع نخواهد شد.
به ظاهر چنین به نظر می رسد که خود این اعلامیه ثابت میکند که تمرین هرگز انجام نخواهد گرفت. به زبان دیگر اجرای تمرین عملی نیست مگر این که به متن اعلامیه عمل نشود.
پارادوکس درریاضی
در ریاضیات نیز میتوان به یک پارادوکس مهم در نظریه مجموعه ها به نام پارادوکس راسل اشاره کرد:
مجموعهA را مجموعه ای تعریف می کنیم که شامل اعضای خود نباشد .یعنی 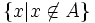
در این صورت اگر 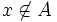 انگاه
انگاه 
اگر 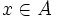 انگاه
انگاه 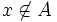
که این پارادوکس از معروفثرین پارادوکس ها در نظریه مجموعه هامی باشد
منطق فازی
ریاضیات فازی یک فرا مجموعه از منطق بولی است که بر مفهوم درستی نسبی، دلالت می کند. منطق کلاسیک هر چیزی را بر اساس یک سیستم دوتائی نشان می دهد ( درست یا غلط، 0 یا 1، سیاه یا سفید) ولی منطق فازی درستی هر چیزی را با یک عدد که مقدار آن بین صفر و یک است نشان می دهد. مثلاً اگر رنگ سیاه را عدد صفر و رنگ سفید را عدد 1 نشان دهیم، آن گاه رنگ خاکستری عددی نزدیک به صفر خواهد بود. در سال 1965، دکتر لطفیزاده نظریه سیستمهای فازی را معرفی کرد. در فضایی که دانشمندان علوم مهندسی به دنبال روشهای ریاضی برای شکست دادن مسایل دشوارتر بودند، نظریه فازی به گونهای دیگر از مدلسازی، اقدام کرد.

منطق فازی معتقد است که ابهام در ماهیت علم است. بر خلاف دیگران که معتقدند که باید تقریبها را دقیقتر کرد تا بهرهوری افزایش یابد، لطفیزاده معتقد است که باید به دنبال ساختن مدلهایی بود که ابهام را به عنوان بخشی از سیستم مدل کند. در منطق ارسطویی، یک دستهبندی درست و نادرست وجود دارد. تمام گزارهها درست یا نادرست هستند. بنابراین جمله «هوا سرد است»، در مدل ارسطویی اساساً یک گزاره نمیباشد، چرا که مقدار سرد بودن برای افراد مختلف متفاوت است و این جمله اساساً همیشه درست یا همیشه نادرست نیست. در منطق فازی، جملاتی هستند که مقداری درست و مقداری نادرست هستند. برای مثال، جمله "هوا سرد است" یک گزاره منطقی فازی میباشد که درستی آن گاهی کم و گاهی زیاد است. گاهی همیشه درست و گاهی همیشه نادرست و گاهی تا حدودی درست است. منطق فازی میتواند پایهریز بنیانی برای فنآوری جدیدی باشد که تا کنون هم دستآوردهای فراوانی داشته است.
کاربردها:
از منطق فازی برای ساخت کنترل کننده های لوازم خانگی از قبیل ماشین رختشویی (برای تشخیص حداکثر ظرفیت ماشین، مقدار مواد شوینده، تنظیم چرخهای شوینده) و یخچال استفاده می شود. کاربرد اساسی آن تشخیص حوزه متغیرهای پیوسته است. برای مثال یک وسیله اندازه گیری دما برای جلوگیری از قفل شدن یک عایق ممکن است چندین عضو مجزا تابعی داشته باشد تا بتواند حوزه دماهایی را که نیاز به کنترل دارد به طور صحیح تعریف نماید. هر تابع، یک ارزش دمایی مشابه که حوزه آن بین 0 و 1 است را اختیار می کند. از این ارزشهای داده شده برای تعیین چگونگی کنترل یک عایق استفاده می شود.
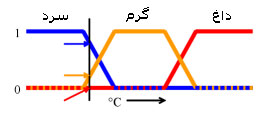 |
در شکل روبرو، سرد بودن، گرم بودن و داغ بودن، توابعی برای مقایسه درجه حرارت هستند و هر نقطه ای روی این خطوط می تواند دارای یکی از سه ارزش بالا باشد. به عنوان مثال برای یک درجه حرارت خاص که در شکل با یک خط نشان داده شده است، می توان گفت: «مقداری سرد است»،«اندکی گرم است» یا «اصلاً داغ نیست».
حال با مثال دیگری اهمیت این علم را بیشتر درک مینمائیم:
یک انسان در نور کافی قادر به درک میلیونها رنگ میباشد.ولی یک روبوت چگونه میتواند این تعداد رنگ را تشخیص دهد؟ حال اگر بخواهیم روباتی طراحی کنیم که قادر به تشخیص رنگها باشد از منطق فازی کمک میگیریم و با اختصاص اعدادی به هر رنگ آن را برای روبوت طراحی شده تعریف میکنیم.
از کاربردهای دیگر منطق فازی میتوان به کاربرد این علم در صنعت اتومبیل سازی(در طراحی سیستم ترمز ABS و کنترل موتور برای بدست آوردن بالاترین راندمان قدرت)،در طراحی بعضی از ریزپردازنده ها و طراحی دوربینهای دیجیتال اشاره کرد.
[ شنبه 87/2/7 ] [ 4:35 عصر ] [ مهندسی مکانیک(امین احمدی) ]
سلام سایت www.3RF2008.com افتتاح شدبزرگترین مقسوم علیه مشترک |
تعریف:
مقسوم علیه های مشترک میان دو عددa وb، اعدادی هستند که بتوانند هم a و هم b را بشمارند به عبارت ریاضی: اگر c مقسوم علیه مشترک دو عدد a و b باشد، آنگاه c|a و c|b .
مثلا مقسوم علیه های دو عدد 15 و30 را داریم:
{15={1,3,5,15}
30={1,2,3,5,6,10,15,30}
مقسوم علیه های مشترک میان این دو عدد عبارتند از:
مقسوم علیه های مشترک:{1,3,5,15}
بزرگترین مقسوم علیه مشترک میان دو عدد، عددی است که نسبت به تمام مقسوم علیه های مشترک میان دو عدد، بزرگترین باشد. به عبارت ریاضی: اگر d بزرگترین مقسوم علیه باشد، d|a و d|b و dبزرگتر از c باشد.
بزرگترین مقسوم علیه مشترک میان این دو عدد ، 15 است. که آن را به این صورت نمایش می دهند:
(15,30)=15
بزرگترین مقسوم علیه میان دو عدد را به اختصار به صورت " ب.م.م " می نویسند.
اگر ب.م.م دو عدد یک باشند ، آنگاه این دو عدد نسبت به هم اولند.مثلا دو عدد 13 و 8 هیچ مقسوم علیه مشترکی جز یک ندارند.
قضایای مربوط به بزرگترین مقسوم علیه مشترک:
قضیه1) این قضیه به قضیه بزو نیز معروف است. مطابق این قضیه مجموعه زیر مجموعه ای از مقسوم علیه های مشترک میان دو عدد a وb هستند:S={m,n ? Z| am+bn>0}
نتیجه ای که از این قضیه می توان گرفت آن است که بزرگترین مقسوم علیه مشترک میان دو عدد aو b مطابق فرمول زیر است:
Am+bn=d.
قضیه 2) d بزرگترین مقسوم علیه مشترک دو عدد a و b است اگر و فقط اگر :
الف) d|a و d|b و ب) اگر c|a و c|b آنگاه c|d.
قضیه 3) اگر a|bc و (a,b)=1 یعنی نسبت به هم اول باشند، آنگاه a|c . این قضیه به لِم اقلیدوس نیز معروف است.
قضیه4) اگر P|ab (P یک عدد اول است)، آنگاه P|a یا P|b .
قضیه5) اگر c کوچکترین مضرب مشترک و d بزرگترین مقسوم علیه مشترک دو عدد a وb باشد آنگاه داریم:
Then: d*c=ab
لم های مربوط به بزرگترین مقسوم علیه های مشترک:
لم 1) بر اساس اصول بنیادی حساب، هر عدد مرکب را می توان به صورت حاصلضرب اعداد اول تجزیه کرد. ب.م.م میان دو عدد برابر با حاصلضرب اعداد اول مشترک میان آن دو عدد به توان عدد کمتر.لم 2) ب.م.م دو عدد، هر مقسوم علیه مشترک میان دو عدد را می شمارد:
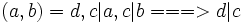
لم 3) اگر
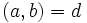 آنگاه :
آنگاه : 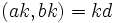
لم 4) اگر
a|c & b|c , (a,b)=1 ===> ab|c
لم 5) اگر
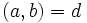 آنگاه
آنگاه 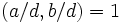
مثال مربوط به بزرگترین مقسوم علیه مشترک :
مثال1) اگر n عددی فرد باشد ثابت کنید که 24حاصلضرب سه عدد متوالی قبل و بعد از n را می شمرد:
24|(n-1)n(n+1)
جواب:
عدد سه، حاصلضرب سه عدد متوالی را می شمرد( اثبات آن به عهده خواننده است. راهنمایی : هر عددی را می توان به صورت :
A=3q+r 0?r<3) 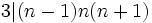
باید ثابت کنیم که حاصلضرب دو عدد زوج متوالی بر 8 تقسیمپذیر است: 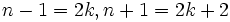 :
:
then: 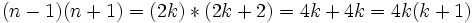
حاصلضرب دو عدد متوالی همواره بر 2 بخش پزیر است.پس: 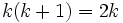
then: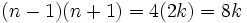
then: 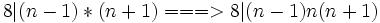
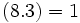 then:
then:
طبق لم 4 داریم: 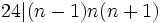
اعداد اول
تعریف:عدد طبیعی p>1,pرا اول می نامند به شرطی که تنها مقسوم علیه های مثبت آن 1وp باشند. اگرعددی طبیعی وبزرگتر از 1اول نباشد مرکب است.
قضیه 1: تعداد اعداد اول نامتناهی است.
برهان: حکم را به روشی که منسوب به اقلیدس است اثبات می کنیم: فرض کنید تعداد اعداد اول متناهی و تعداد آنها n تا باشد . حال عدد M را که برابر حاصلضرب این اعداد به علاوه ی 1 را در نظر بگیرید. این عدد مقسوم علیهی غیر از آن n عدد دارد که با فرض در تناقض است.
(البته شایان ذکر است که این قضیه اثبات های گوناگونی دارد که ما ساده ترین آنها را انتخاب کردیم اگر مایلید می توانید اثبات های دیگر آن را بیاورید.)
قضیه 2:قضیه ی اساسی حساب: هر عدد طبیعی بزرگتر از 1 را به شکل حاصلضرب اعدادی اول نوشت.
قضیه 3: قضیه چپیشف:اگر n عددی طبیعی و بزرگتر از 2 باشد, حتما" بین n و 2n عدد اولی وجود دارد. (شخصا" توصیه میکنم از اثبات کردن این قضیه خودداری کنید)
همنهشتی |
تعریف:
اگر m یک عدد طبیعی و a وb دو عدد صحیح باشند، و m بتواند اختلاف بین aوb را بشمارد، آنگاه می گوییم a همنهشت با a است به پیمانه m.
رابطه همنهشتی یک رایطه هم ارزی است پس این رابطه می تواند مجموعه Z را افراز کند. به مثال 2 در این زمینه توجه کنید.
ویژگی های همنهشتی:
- اگر b?a به پیمانه m آنگاه داریم:
A+c?b+c و بلعکس
- اگر
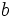 و
و 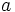 باهم همنهشت و
باهم همنهشت و 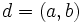 و
و  به همنهشت به پیمانه m آنگاه داریم:
به همنهشت به پیمانه m آنگاه داریم:
ac?bc به پیمانه m
- اگر b?a به پیمانه m داشته باشیم آنگاه به ازای n های طبیعی داریم:
 و
و  با هم همنهشتند به پیمانه m
با هم همنهشتند به پیمانه m
- اگر به ازای تمام aوb های همنهشت به پیمانه m داشته باشیم،آنگاه مجموع و حاصلضرب متناظرشان نیز باهم همتهشتند به پیمانه m.
- اگر b?a به پیمانه m داشته باشیم و c عدد صحیحی باشد، آنگاه داریم:
ac?bc به پیمانه m.
قضایای مربوط به همنهشتی:
قضیه 1) اگر ac?bc به پیمانه m و آنگاه داریم:
آنگاه داریم:
a?b به پیمانه m/d
لم مربوط به همنهشتی:
لم1) اگر a?b به پیمانه m باشد و d یکی ازمقسوم علیه های m باشد آنگاه داریم:
a?b به پیمانه d
لم2) اگر  و
و  باهم همنهشت به پیمانه m و
باهم همنهشت به پیمانه m و آنگاه داریم:
آنگاه داریم:
a?b به پیمانه m
لم 3) اگر r باقیمانده تقسیم a بر m باشد، انگاه، a?r به پیمانه m.
مثال مربوط به همنهشتی:
مثال1) 36همنهشت با18 به پیمانه 6. یعنی 36-18=18 و 18|6 و به عبارتی دیگر،8 بر 6 بخش پذیر است.
مثال2) مجموعه اعدادی را بیابید که اختلافشان بر عدد 2 بخش پذیر باشد.
جواب:
تمام اعداد صحیح بخش پذیر بر 2 عبارتند از:
A=2q+r 0?r<2
پس داریم:
A=2q and a=2q+1
{  به طوری که اختلاف این اعداد با عدد 2، همواره بر 2 بخش پذیر است. یعنی می توان گفت x1?x2 به پیمانه 2.
به طوری که اختلاف این اعداد با عدد 2، همواره بر 2 بخش پذیر است. یعنی می توان گفت x1?x2 به پیمانه 2.
و همچنین داریم:
{  }
}
به طوری که اختلاف این اعداد با عدد 2، همواره بر 2 بخش پذیر است. یعنی می توان گفت z1?z2 به پیمانه 2.
اعداد اول |
تعریف:عدد طبیعی p>1,pرا اول می نامند به شرطی که تنها مقسوم علیه های مثبت آن 1وp باشند. اگرعددی طبیعی وبزرگتر از 1اول نباشد مرکب است.
قضیه 1: تعداد اعداد اول نامتناهی است.
برهان: حکم را به روشی که منسوب به اقلیدس است اثبات می کنیم: فرض کنید تعداد اعداد اول متناهی و تعداد آنها n تا باشد . حال عدد M را که برابر حاصلضرب این اعداد به علاوه ی 1 را در نظر بگیرید. این عدد مقسوم علیهی غیر از آن n عدد دارد که با فرض در تناقض است.
(البته شایان ذکر است که این قضیه اثبات های گوناگونی دارد که ما ساده ترین آنها را انتخاب کردیم اگر مایلید می توانید اثبات های دیگر آن را بیاورید.)
قضیه 2:قضیه ی اساسی حساب: هر عدد طبیعی بزرگتر از 1 را به شکل حاصلضرب اعدادی اول نوشت.
قضیه 3: قضیه چپیشف:اگر n عددی طبیعی و بزرگتر از 2 باشد, حتما" بین n و 2n عدد اولی وجود دارد. (شخصا" توصیه میکنم از اثبات کردن این قضیه خودداری کنید)
تئوری اعداد
تئوری اعداد number theory شاخه ای از ریاضیات محض pure mathematics است که در مورد خواص اعداد صحیح integers بحث می کند و حاوی بسیاری مسائل است که حتی غیر ریاضیدانان به راحتی آنها را متوجه می شوند .به طور کلی ایـن شاخه ، مسائل مربوط به مطالعه اعداد صحیح را مطرح می کند. تئوری اعداد را می توان بنا به روشهای بررسی سؤالات به چندین بخش تقسیم کرد. مثلاً به سرفصل های تئوری اعداد مراجعه نمایید .

-
تئوری مقدماتی اعداد ،اعداد صحیح را بدون توجه به تکنیک های ریاضی به کار رفته در سایر شاخه ها بررسی می کند . مسائل بخشپذیری divisibility ، الگوریتم اقلیدسیEuclidean algorithm ، محاسبه ی بزرگترین مقسوم الیه مشترک greatest common divisors ، تجزیه ی اعداد به اعداد اول prime numbers ، جستجوی عدد تام perfect number و همنهشتی ها congruences در این رده هستند . نمونه ها قضیه ی کوچک فرما Fermat’s little theorem ، و قضیه ی اولر Euler’s theoremهستند و به طور عام قضیه ی باقیمانده ی چینی Chinese remainder theorem و قانون تقابل درجه ی دوم quadratic reciprocity هستند . خواص توابع ضربیmultiplicative functions مانند تابع موبیوس Mobius function و تابع اولر Euler"s ? function و همینطور دنباله ی اعداد صحیح integer sequences مانند فاکتوریل هاfactorials و اعداد فیبوناچی Fibonacci numbers در همین حوزه بررسی میشوند . بسیاری از سؤالات در تئوری مقدماتی اعداد شدیداً عمیق هستند و نیاز به بازنگری هایی دارند . به عنوان نمونه :
-
انگارهی گلدباخ Goldbach conjecture که میگوید آیا هر عدد زوجی حاصلجمع دو عدد اول است یا نه.
-
انگارهی کاتالان Catalan’s conjecture که در مورد توانهای متوالی اعداد صحیح است .
-
انگارهی اعداد اول دوقلو Twin prime conjecture که در مورد بینهایت بودن اعداد اول دوقلو است.
-
انگارهی کولاتز Collatz conjecture که در مورد تکرار ساده میباشد .
-
معادلات دیوفانتیDiophantine نیز هنوز تصمیم ناپذیر است.
-
تئوری تحلیلی اعداد Analytic number theory ازحسابانcalculus و آنالیز مختلطcomplex analysis برای مطالعهی اعداد صحیح استفاه می کند و با سؤالاتی در مورد اعداد صحیح دست و پنجه نرم می کند که در تئوری مقدماتی اعداد بررسی و بحث در مورد آن بسیار دشوار به نظر میرسد . قضیه ی اعداد اولprime number theorem و فرضیه ریمان Riemann hypothesis مثال هایی از آن هستند . مسئله ی وارینگ Waring’s problem ( که عدد صحیحی را به صورت جمع چند مربع یا مکعب چند عدد نشان می دهد ) ،انگارهی اعداد اول دوقلو Twin prime conjecture(که تعداد بینهایت عدد اول با اختلاف 2 را پیدا می کند ) ، و فرضیه ی گلدباخGoldbach’s conjecture ( که عددهای زوج داده شده را به صورت مجموع دو عدد اول پیدا می کند ) با روشهای تحلیلی مورد حمله قرار گرفته شده اند . اثبات متعالی بودن transcendence ثابت های ریاضی ، مانند e و پی در بخش تئوری اعداد تحلیلی قرار دارند . بعضی ها حکم هایی در مورد اعداد متعالی را از محدوده ی مطالعات اعداد صحیح خارج می کنند ، در واقع مقادیر ممکن برای چند جمله ایها با ضریب های صحیح مانند e و پی به مبحث تقریب دیوفانتین Diophantine aproximation ارتباط نزدیک دارند ؛ و سؤال آنها این است که چگونه می توان یک عدد حقیقی داده شده را با یک عدد گویا rational تقریب زد ؟
-
تئوری جبری اعداد ، مفهوم عدد را به اعداد جبری algebraic numbers که همان ریشه های چند جمله ایها با ضرایب گویا rational coefficient هستند گسترش میدهد.در این حوزه مباحثی همانند اعداد صحیح به نام اعداد صحیح جبری algebraic integers وجود دارد . در اینجا لازم نیست به صورت های آشنای اعداد صحیح ، ( مانند تجزیه یکتا the unique factorization) پایبند باشیم .مزیت روش استفاده شده --تئوری گالوا Galois theory ، میدان همانستگی field cohomology ، تئوری رده ی میدان class field theory ، نمایش گروه ها group representations و L-تابعها L-functions این است که به ما اجازه می دهدبرای این رده از اعداد ، این ترتیب را تا حدودی بپوشانیم .تعدادی از سؤالات قضیه ی اعداد با مطالعه پیمانه p برای کلیه اعداد اول p مورد حمله قرار گرفته شده اند . (به میدانهای متناهی finite fields مراحعه کنید ) .به چنین چیزی localization می گویند که به ساختمان اعداد p ادیک p-adic numbers می انجامد . به این محدوده تحلیل موضعی local analysis می گویند که از تئوری اعداد جبری ناشی می شود .
-
تئوری ترکیبیاتی اعداد به بررسی ، مطالعه و حل مسالههای تئوری اعداد با استفاده از تکنیکهای ترکیبیاتی میپردازد. پل اردوش کارهای بزرگی در این زمینه انجام داد. روشهای جبری و تحلیلی در این شاخه از تئوری اعداد کاربرد فراوان دارند.
-
تئوری هندسی اعداد همه ی فرم های هندسی را در بر می گیرد ؛و از قضیه ی مینکوسکی Minkowski’s theorem در ارتباط با نقاط مشبکه lattice points در مجموعه های محدب convex sets و جستجو در بسته بندی کره ها sphere packings شروع می شود .هندسه جبری بخصوص خمهای بیضویelliptic curves نیز به کار می آیند .این تکنیکها در اثبات آخرین قضیه معروف فرما Fermat’s last theorem تاثیر فراوان داشته اند .
-
تئوری محاسباتی اعداد computational number theory به الگوریتم های تئوری اعداد می پردازد والگوریتم های سریع برای امتحان اعداد اول prime testing و تجزیه اعداد صحیح integer factorization در مبحث کریپتوگرافی cryptography کاربرد های مهمی دارند .
.
 |
تاریخچه تئوری اعداد
چبیشفChebyshev کران هایی برای تعداد اعداد اول بین یک بازه ارائه داد . ریمان Riemann اظهار کرد که حد تعداد اعداد اول از یک عدد داده شده تجاوز نمی کند . (قضیه ی عدد اول prime number theory. ) و آنالیز مختلط complex analysis را در تئوری تابع زتای ریمان Riemann zeta function گنجاند و فرمول صریح تئوری اعداد اول explicit formulae of prime number theory را از صفر های آن نتیجه گرفت .
تئوری همنهشتی congruences از Disquisitiones گاوس شروع شد . او علامت گذاری زیر را پیشنهاد کرد :
چبیشف در سال 1847 به زبان روسی کاری را در این زمینه منتشر کرد و سره Serret آن را در فرانسه عمومی کرد . بجای خلاصه کردن کارهای قبلی ، لوژاندر قانون تقابل درجه ی دوم law of quadratic reciprocity را گذاشت . این قانون از استقراء induction کشف شد و قبلاً اولر آن را مطرح کرده بود. لوژاندر در تئوری اعداد Théorie des Nombres برای حالت های خاص آن را ثابت کرد . جدا از کارهای اولر و لوژاندر ، گاوس این قانون را در سال 1795 کشف کرد و اولین کسی بود که یک اثبات کلی ارائه داد . کوشی Cauchy ؛ دیریکله Dirichlet ( که مقاله ی Vorlesungen über Zahlentheorie او یک مقاله ی کلاسیک است) ؛ ژاکوبی Jacobi که علامت ژاکوبی Jacobi symbol را معرفی کرد ؛ لیوویلLiouville ؛ زلرZeller ؛ آیزنشتین Eisenstein؛ کومرKummer و کرونکر Kronecker نیز در این زمینه کارهایی کرده اند . این تئوری تقابل درجه دوم و سوم cubic and biquadratic reciprocity را شامل می شود. نمایش اعداد با صورت درجه ی دوم دوتایی binary quadratic forms مدیون گاوس است . کوشی ، پوانسو Poinsot ، لبگ Lebesgue و بخصوص هرمیت Hermite به موضوع چیزهایی افزوده اند . آیزنشتاین Eisenstein در تئوری صورت های سه گانه پیشتاز است ، و تئوری فرمها theory of forms به طور کلی مدیون او و اچ. اسمیتH. J. S. Smith است. اسمیت دسته بندی کاملی از صورتهای سه گانه انجام داد و تحقیقات گاوس در مورد صورت های درجه ی دوم حقیقی به فرمهای مختلط افزود . جستجوهایی در مورد نمایش اعداد به صورت جمع 4، 5 ،6 ، 7 ، 8 ، مربع توسط آیزنشتاین ادامه یافت و اسمیت آن را کامل کرد .
[ شنبه 87/2/7 ] [ 4:34 عصر ] [ مهندسی مکانیک(امین احمدی) ]
-
سلام سایت www.3RF2008.com افتتاح شد
-
-
-
-
حساب <<حسابداری): جهت مشاهده مفهوم حساب در حسابداری.
-
حساب دیفرانسیل و انتگرال: جهت مشاهده علم حساب.
در ریاضیات، تابع رابطه ای است که رابطه بین اعضای یک مجموعه را با اعضایی از مجموعه ای دیگر (شاید یک عضو از مجموعه) را بیان می کند. نظریه درباره تابع یک پایه اساسی برای خیلی از شاخه های ریاضی به حساب می آید.
مفاهیم تابع، نگاشت و تبدیل معمولاً مفاهیم مشابه ای هستند. عملکرد ها معمولاً دو به دو بین اعضای تابع وارد عمل می شوند.
تعریف:
تابع یک قاعده ای است که ورودیهایی را می گیرد و خروجیهایی را به ما پس می دهد. مثالهایی را ذکر می کنیم.
-
هر شخص دارای هشت رنگ مورد علاقه دارند (قرمز، نارنجی، زرد، سبز، آبی، بنفش، نیلی، صورتی) رنگ مورد علاقه یک تابع انسانی است. برای مثال علی رنگ قرمز را دوست دارد. در حالی که کیارش رنگ بنفش را دوست دارد.در اینجا، ورودی یک مشخص است ولی خروجی یکی از هشت رنگ است. باید به نکته توجه کرد که چند شخص می توانند یک رنگ را انتخاب کنند.
-
یک سنگ از طبقات مختلف یک ساختمان رها می شود. این سنگ در 2 ثانیه، 2 طبقه را پائین می رود و در 4 ثانیه، 8 طبقه را پایین می رود. در اینجا، طبقات به عنوان ورودی و تعداد ثانیه ها به عنوان خروجی به حساب می آیند.
قاعده تعریف یک تابع می تواند به وسیله یک فرمول، رابطه و یا یک جدول ساده که ورودیها و خروجیها را در برابر هم قرار می دهد، باشد.
در توابع، ورودیها به عنوان متغیر تابع و خروجیها به عنوان ارزش تابع شناخته می شوند.
یک نمونه از توابع، توابعی است که رابطه متغیر تابع با ارزش تابع به صورت یک فرمول بیان می شود. و ارزش تابع از جایگزین متغیر در فرمول بدست می آید.
به عنوان مثال تابع
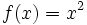
بیان می کند که ارزش تابع برابر است با مربع هر عددی مانند x
 |
تعریف روی مجموعه ها
یک تابع رابطهای منحصر به فرد است که یک عضو از مجموعه ای را با اعضای مجموعهای دیگر مرتبط میکند.
تمام روابط موجود بین دو مجموعه نمی تواند یک تابع باشد برای روشن شدن موضوع، مثالهایی در زیر ذکر می کنیم:
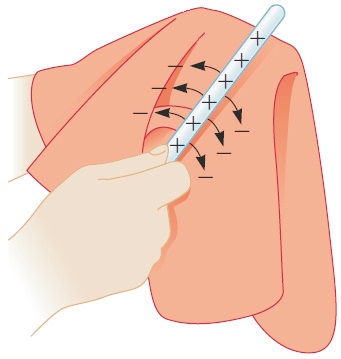 |
-
این رابطه یک تابع نیست چون در آن عنصر 3، با دو عنصر ارتباط دارد. که این با تعریف تابع متناقص است چون برای یک عنصر از مجموعه، دو عنصر در مجموعه موجود است
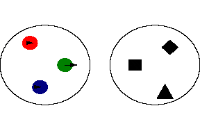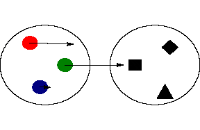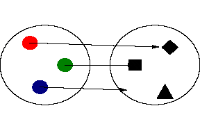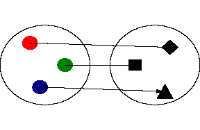 |
-
این رابطه یک تابع یک به یک است. چون به ازای هر x یک y وجود دارد
خواص توابع
توابع می توانند:
-
زوج یا فرد باشند.
-
پیوسته یا ناپیوسته باشند.
توابع چند متغیره:
یک تابع ممکن است بیشتر از یک متغیر داشته باشد برای مثال  یک تابع از f است که دارای سه پارامتر x,y,z است که یک ارزش را برای تابع تولید می کنند. از توابع چند متغیره می توان به قانون جاذبه نیوتن اشاره کرد که در آن دو جرم با متغیر
یک تابع از f است که دارای سه پارامتر x,y,z است که یک ارزش را برای تابع تولید می کنند. از توابع چند متغیره می توان به قانون جاذبه نیوتن اشاره کرد که در آن دو جرم با متغیر 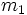 و
و 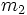 و نیز یک متغیر برای فاصله هر جرم به نام
و نیز یک متغیر برای فاصله هر جرم به نام 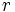 در آن وجود دارد.
در آن وجود دارد.
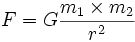
با مقدار دهی به سه پارامتر فوق مقدار تابع F محاسبه خواهد شد.
- تاریخچه
- قلمرو امروزی حساب دیفرانسیل و انتگرال
- بزرگان این علم
حسابیا حساب دیفرانسیل و انتگرال ریاضیات مربوط به حرکت و تغییر است.
حساب دیفرانسیل و انتگرال
تاریخچه
حساب دیفرانسیل و انتگرال در آغاز برای براورده کردن نیازهای دانشمندان قرن 17 ابداع شد.البته لازم به ذکر است ریشه های این علمرا میتوان تا هندسه کلاسیک یونانی میتوان ردیابی کرد
حساب دیفرانسیل و انتگرال به دانشمندان امکان می داد شیب خمها را تعریف کنند، زاویه آتشباری توپ را برای حصول بیشترین برد بدست آورند،و زمانهایی که سیارات نزدیکترین و دورترین فاصله را از هم دارند،پیش بینی کنند.
پیش از پیشرفتهای ریاضی که به کشف بزرگ آیزاک نیوتن و لایب نیتس انجامید،یوهانس کپلر منجم با بیست سال تفکر،ثبت اطلاعات،و انجام محاسباث سه قانون حرکت سیارات را کشف کرد:
 |
|
|
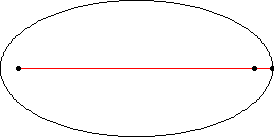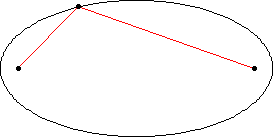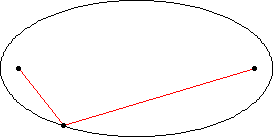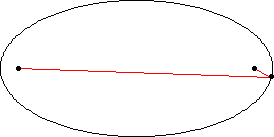
1.هر سیاره در مداری بیضی شکل حرکث میکندکه یک کانونش در خورشید است
2.خط واصل بین خورشید و ستاره در مدتهای مساوی مساحات مساوی را طی میکنند
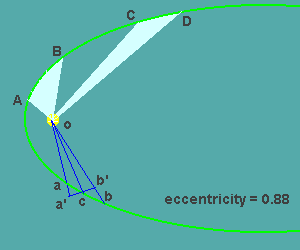 |
|
|
3.مربع گردش هر سیاره به دور خورشید،متناسب است با مکعب فاصله متوسط آن سیاره از خورشید
ولی استنتاج قوانین کپلر از قوانین حرکت نیوتن با استفاده از حساب دیفرانسیل و انتگرال کار ساده ای است.
قلمرو امروزی حساب دیفرانسیل و انتگرال
امروز حساب دیفرانسیل و انتگرال در آنالیز ریاضی قلمرو واقعا گسترده ای دارد و فیزیکدانان و ریاضیدانان که اول بار این موضوع را ابداع کردند مسلما شگفت زده و شادمان می شدند اگر می دیدند که این موضوع چه انبوهی از مسائل را حل میکند.
امروزه اقتصاددانان از حساب دیفرانسیل و انتگرال برای پیش بینی گرایشهای کلی اقتصادی استفاده می کنند. اقیانوس شناسان برای فرمول بندی نظریه هایی درباره جریانهای دریایی بهره میگیرند،و هواشناسان آن را برای توصیف جریان هوای جو به کار میگیرند،دانشمندان علوم فضایی آن را برای طراحی موشکها به کار میبرند.روانشناسان از آن برای درک ثوهمات بصری استفاده می کنندو...
به طور خلاصه حساب دیفرانسیل و انتگرال علمی است که درتمام علوم امروزی کاربرد بسزایی دارد.
بزرگان این علم
این علم عمدتا کار دانشمندان قرن هفدهم اسث. از میان این دانشمندان میتوان به رنه دکات ،کاوالیری،فرما
و جیمز گرگوری اشاره کرد.
پیشرفت حساب دیفرانسیل و انتگرال در قرن 18 با سرعت زیادی ادامه یافت، در زمره مهمترین افرادی که در این زمینه سهم داشتند میتوان به برادران برنولی اشاره کرد.در واقع خانواده برنولی همان نقشی را در ریاضیات داشتند که خانواده باخ در موسیقی ایفا کردند.
تکمیل ساختار منطقی روشهای حساب دیفرانسیل و انتگرال را ریاضیدانان قرن 19 از جمله لوئی کوشی و کارل وایرشتراس
بر عهده گرفتند.
مطلب را با سخنی از جان فون نویمان که از ریاضیدانان بزرگ قرن بیستم است به پایان میبریم « حساب دیفرانسیل و انتگرال نخستین دستاورد ریاضیات نوین است و درک اهمیت آن کار آسانی نیست. به عقیده من،این حساب روشنتر از هر مبحث دیگری مرحله آغازی ریاضیات نوین را توصیف می کند؛و نظام آنالیز ریاضی، که توسیع منطقی آن است،هنوز بزرگترین پیشرفت فنی در تفکر دقیق به شمار می آید.»
حساب برداری |
حساب برداری، شاخه ای از علم ریاضیات است که بردارهای چند متغیره را در فضاهای دو بسیاری از نتایج تحلیلی بعدی و یا چند بعدی مورد بررسی قرار می دهد و شامل فرمولها و روش های حل مسئله زیادی است که در مهندسی و فیزیک کاربر فراوان دارد ـ بحث ما درباره بردارها و ارتباط یک بردار با زمینه های اسکالر آن و نیز عکس آن است. به عنوان مثال دمای یک استخر نشان دهنده یک کمیت عددی (اسکالر) است و هر نقطه ای از آب درون آن، دارای یک درجه حرارت است ولی آب جاری درون استخر را می توانیم یک فضای برداری در نظر گرفته و هر نقطه ای از آن را با یک بردار سرعت نشان دهیم. سه عملکرد زیر مهمترین اجزاء حساب برداری هستند:
مهمترین قضایای این مبحث مهم ریاضی عبارتند از:
بسیاری از نتایج تحلیلی بدست آمده در این مبحث، براحتی قابل فهم هستند و در هندسه دیفرانسیل از آن استفاده می شود.
در ریاضیات، مفهوم حد، برای بیان رفتار یک تابع مورد استفاده قرار می گیرد و به بررسی این رفتار در نقاط روی صفحه و یا در بی نهایت می پردازد. حد در حساب دیفرانسیل و انتگرال و نیز در آنالیز ریاضی برای تعریف مشتق و نیز مفهوم پیوستگی مورد استفاده قرار می گیرد.
حد تابع در یک نقطه
اگر یک تابع و یک عدد حقیقی باشد و داشته باشیم: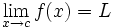 آن گاه این فرمول را چنین میخوانیم << حد تابع f وقتی که x به سمت می رود برابر L است>> توجه کنید که این عبارت حتی اگر
آن گاه این فرمول را چنین میخوانیم << حد تابع f وقتی که x به سمت می رود برابر L است>> توجه کنید که این عبارت حتی اگر 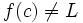
باشد نیز می تواند درست باشد. در عوض تابع در نقطه c تعریف نشده است.حالی مثالی را ذکر می کنیم:تابع زیر را در نظر میگیریم 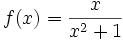
حال متغیر x را به عدد2 نزدیک می کنیم و خواهیم دید که مقدار تابع به 0.4 نزدیک می شود. در این مورد مشاهده می شود که 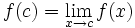 در این صورت گزینه تابع در نقطه X=C دارای
در این صورت گزینه تابع در نقطه X=C دارای
پیوستگی است. اما همیشه این مورد برقرار نیست.
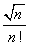 |
|
|
تعریف مجرد حد:
فرض کنید f تابعی باشد روی یک بازه باز که شامل نقطه C است و فرض کنید L یک عدد حقیقی باشد در این صورت 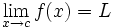 را به صورت زیر تعریف میکنیم:
را به صورت زیر تعریف میکنیم:
به ازای هر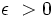 وجود دارد یک
وجود دارد یک  که برای هر x دلخواه اگر
که برای هر x دلخواه اگر 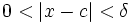 آنگاه نتیجه بگیریم:
آنگاه نتیجه بگیریم: 
حد توابع در بی نهایت
حد یک تابع فقط در نزدیکی اعداد متناهی تعریف نمی شود بلکه ممکن است متغیر توابع وقتی که بی نهایت نزدیک می شود دارای حد باشند.به عنوان مثال در تابع
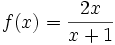 خواهیم داشت:
خواهیم داشت: - f(100) = 1.9802
- f(1000) = 1.9980
- f(10000) = 1.9998
مشاهده میشود که هر چه قدر x بزرگتر میشود ،مقدار تابع به عدد 2 نزدیکتر میشود .در واقع داریم: 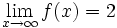
حد یک دنباله
حد یک دنباله مانند 1.79, 1.799, 1.7999,... را در نظر بگیرید. مشاهده می کنیم که این دنباله به عدد 1.8 نزدیک می شود.به طور کلی فرض می کنیم یک دنباله از اعداد حقیقی باشد. می گوییم حد این دنباله برابر L است و می نویسیم:
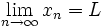 اگر و تنها اگر برای هر
اگر و تنها اگر برای هر 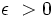 یک عدد طبیعی مانند m باشد که برای هر n>m داشته باشیم
یک عدد طبیعی مانند m باشد که برای هر n>m داشته باشیم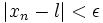
باید توجه کرد که ما می توانیم مقدار
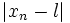 . را به عنوان فاصله بین
. را به عنوان فاصله بین 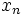 و L در نظر بگیریم به چنین دنباله هایی که حد آنها به یک عدد متناهی میل می کند همگرا گویند و گرنه به آن واگرا گویند.
و L در نظر بگیریم به چنین دنباله هایی که حد آنها به یک عدد متناهی میل می کند همگرا گویند و گرنه به آن واگرا گویند.[ شنبه 87/2/7 ] [ 4:33 عصر ] [ مهندسی مکانیک(امین احمدی) ]
سلام سایت www.3RF2008.com افتتاح شد
جبر از کلمه عربی <<الجبر>> به معنای به هم پیوستگی و یااتصال گرفته شده است.جبر شاخه از ریاضیات است که علم حساب را وسعت می بخشد.وروابط میان کمیت های یک مجموعه را بیان میکندو به طور کلی از تقسیم بندی زیر تبعیت میکند:
1.جبر پایه:در این شاخه از جبر ویژگیهای اعمال چهارگانه در دستگاه اعداد حقیقی ثبت میشود.علائمی تعریف میشوند که بوسیله آن اعداد ثابت و متغیرها از هم تفکیک میگردد و روش هایی که برای حل معادلات مورد استفاده قرار میگیرد.
2.جبر مجرد:در این شاخه ساختارهای جبری از قبیل گروهها، حلقه ها و میدان هاتعریف میشوند و در مورد خصوصیات آنها بحث می شود.
در جبر پیشرفته، مباحثی مانند گروهها ، حلقه ها، میدانها، از دیدگاه توپولوژی طبیعی مورد مطالعه قرار میگیرند.
خوارزمی 
خوارزمی ابو جعفر محمد بن موسی از دانشمندان بزرگ ریاضی و نجوم می باشد از زندگی خوارزمی چندان ا طلاع قابل اعتمادی در دست نیست الا اینکه وی در حدود سال 780 میلادی در خوارزم(خیوه کنونی) متولد شد شهرت علمی وی مربوط به کارهایی است که در ریاضیات مخصوصاٌ در رشته جبر انجام داده به طوری که هیچیک از ریاضیدانان قرون وسطی مانند وی در فکر ریاضی تاثیر نداشته اند اجداد خوارزمی احتمالاٌ اهل خوارزم بودند ولی خودش احتمالاٌ از قطر بولی ناحیه ای نزدیک بغداد بود. به هنگام خلافت ماموی عضو دارالحکمه که مجمعی از دانشمندان در بغداد به سرپرستی مامون بود، گردید خوارزمی کارهای دیونانتوس را در رشته جبر دنبال کرد و به بسط آن پرداخت خود نیز کتابی در این رشته نوشت.
الجبر و المقابله که به مامون تقدیم شده کتابی است در باره ریاضیات مقدماتی و شاید نخستین کتاب جبری باشد که به عربی نوشته شده است دانش پژوهان بر سر این که چه مقدار از محتوای کتاب از منابع یونانی و هندی و عبری گرفته شده است اختلاف نظر دارند معمولاٌ در حل معادلات دو عمل معمول است خوارزمی این دو را تنقیح و تدوین کرد و از این راه به واردساختن جبر به مرحله علمی کمک شایانی انجام داد اثر ریاضی دیگری که چندی پس از جبر نوشته شد رساله ای است مقدماتی در حساب که ارقام هندی(یا به غلط ارقام عربی) در آن به کار رفته بود و نخستین کتابی بود که نظام ارزش مکانی را(که آن نیز از هند بود) به نحوی اصولی و منظم شرح می داد اثر دیگری که به مامون تقدیم شد زیج السند هند بود مه نخستین اثر اختر شناسی عربی است که به صورت کامل بر جای مانده و شکل جداول آن از جداول بطلمیوس تاثیر پذیرفته است. کتاب صورت الارض که اثری است در زمینه جغرافیا اندک زمانی بعد از سال 195 – 196 نوشته شده است و تقریباٌ فهرست طولها و عرضهای همه شهرهای بزرگ و اماکن را شامل می شود این اثر که احتمالاٌ مبتنی بر نقشه جهان نمای مامون است(که شاید خود خوارزمی هم در تهیه آن کار کرده بوده باشد)، به نوبه خود مبتنی بر جغرافیای بطلمیوسی بود این کتاب از بهضی جهات دقیق تر از اثر بطلمیوس بود خاصه در قلمرو اسلام. تنها اثر دیگری که بر جای مانده است رساله کوتاهی است در باره تقویم یهود. خوارزمی دو کتاب نیز در باره اسطرلاب نوشت آثار علمی خوارزمی از حیث تعداد کم ولی از نفوذ بی بدیل برخوردارند زیرا که مدخلی بر علوم یونانی و هندی فراهم آورده اند بخشی از جبر دوبار در قرن ششم / دوازدهم به لاتینی ترجمه شد و نفوذی عمده بر جبر قرون وسطایی داشت رساله خوارزمی در باره ارقام هندی پس از آنکه در قرن دوازدهم به لاتینی ترجمه و منتشر شد بزرگترین تاثیر را بخشید نام خوارزمی مترادف شد با هر کتابی که در باره حساب جدید نوشته می شد(و از اینجا است اصطلاح جدید))الگوریتم)) به معنی قاعده محاسبه کتاب جبر و مقابله خوارزمی که به عنوان الجبرا به لاتینی ترجمه گردید باعث شد که همین کلمه در زبانهای اروپایی به معنای جبر به کار رود نام خوارزمی هم در ترجمه به جای الخوارزمی به صورت الگوریتمی تصنیف گردید و الفاظ آلگوریسم و نظایر آنها در زبانهای اروپایی که به معنی فن محاسبه ارقام یا علامات دیگر است مشتق از آن می باشد.
ارقام هندی که به غلط ارقام عربی نامیده می شود از طریق آثار فیبوناتچی به اروپا وارد گردید همین ارقام انقلابی در ریاپیات به وجود آورد و هر گونه اعمال محاسباتی را مقدور ساخت باری کتاب جبر خوارزمی قرنها در اروپا ماخذ و مرجع دانشمندان و محققین بوده و یوهانس هیسپالنسیس و گراردوس کرموننسیس و رابرت چستری در قرن دوازدهم هر یک از آن را به زبان لاتینی ترجمه کردند نفوذ کتاب زیج السند چندان زیاد نبود اما نخستین اثر از این گونه بود که به صورت ترجمه لاتینی به همت آدلاردباثی در قرن دوازدهم به غرب رسید جداول طلیطلی(تولدویی) یکجا قرار گرفتند و به توسط ژرار کرمونایی در اواخر قرن یازدهم به لاتینی ترجمه شدند، از مقبولیت گستره تری در غرب برخوردار شدند و دست کم یکصد سال بسیار متداول بودند از کارهای دیگر خوارزمی تهیه اطلسی از نقشه آسمان و زمین و همچنین اصلاح نقشه های جغرافیایی بطلمیوس بود جغرافیای وی تا اواخر قرن نوزدهم در اروپا ناشناخته ماند، دیگر از کتب مهم خوارزمی کتاب مفاتیح العلوم است که کتاب مهم و ارزنده ای است خوارزمی در حدود سال 848 میلادی مطابق با 232 هجری قمری در گذشت.
معادله
در ریاضیات، یک معادله از یک یا چندین متغیر تشکیل شده است که میتواند یک یا چندین جواب داشته باشد.در یک معادله دو عبارت در دو سوی یک = قرار دارند.و مقادیری که به ازای آنها دو عبارت موجود،مقداری مساوی دارند را جواب معادله گویند. به عنوان مثال عبارت زیر یک معادله با یک جواب است. 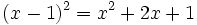
ولی عبارت زیر معادله ای با دو جواب میباشد. 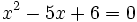
تاریخچه
معادلات همراه با اعداد، از اولین دستاوردهای ریاضی بشرند. آنها در قدیمی ترین اسناد ریاضی، مکتوب، فی المثل، در متون میخی بابلیهای باستان، که به هزاره قبل از میلاد بر می گردند، و پاپیروسهای مصری باستان، که به امپراطوری میانه در حدود 1800 ق.م. بازگشت دارند، آمده اند.
بنا به ساختار جامعه بابلی مسائل مربوط به تقسیم ارث از اهمیت بسیاری برخوردار بودند. اولین پسر همواره بیشترین سهم را دریافت می کرد، دومی بیشتر از سومی، و به همین ترتیب.
در حالی که مسائل مطرح در بابل ،مجهول نسبتاً واضح توصیف شده است، در پاپیروس های مصری با علامت "h" نمایش داده شده است، که توده یا گردایه را نشان می دهد. چنین محاسباتی نسبتاً زیاد رخ می دهند و متناظر با معادلات خطی ما هستند. مقایسه ای بین متنی مصری از پاپیروس مسکو و نماد نویسی جدید این نکته را روشن می سازند.
پیش از این که زبان نمادین جبری مطرح شود، معادلات را بالاجبار با کلمات می نوشتند حتی فرانسواویت که معمولاً به ویتا موسوم است که شایستگی های بسیاری در زمینه جبر دارد از کلمه لاتین برای برابر بودن استفاده می کرد
علامت برابری = که امروزه متداول است توسط روبرت رکورد پزشک دربار سلطنتی مطرح شد، اما زمان قابل ملاحظه ای طول کشید تا این علامت مقبولیت عام یافت.
 |
|
|
وی این طرح را در کتاب درسی جبری که به صورت گفتگو نوشته شده بود و عنوانش "the whetstone of witte" بود مطرح و انگیزه انتخاب ان را با گفتن مطالب زیر بیان کرد «در این مورد همان گونه که قالباً در عمل انجام می دهم یک جفت خط توامان می گذارند این چنین = = =, زیرا هیچ دو شیی نمی توانند برابر محض باشند.
مجموعه جواب
کار با مجموعه معینی از اعداد، موسوم به حوزه اصلی و مجموعه مشخصی از متغیرها که عناصری از حوزه اصلی با زیر مجموعه ای، موسوم به حوزه تغییرپذیری را می توان به جای آنها قرارداد، آغاز می شود.
در مشخص کردن حوزه اصلی و حوزه تغییر پذیری،N به جای مجموعه اعداد طبیعی، Z به جای مجموعه اعداد صحیح،Q به جای مجموعه اعداد گویا،R به جای مجموعه اعداد حقیقی و C به جای اعداد مختلط قرار می گیرد.
گروه
در ریاضیات، گروه، مجموعهای است که یک عمل دوتایی ازقبیل جمع،ضرب و... روی آنها تعریف میکنند.برای مثال مجموعه اعداد صحیح یک گروه تحت عمل جمع است.
شاخهای از ریاضیات که بر روی گروهها مطالعه میکند، نظریه گروهها است.از نظر تاریخی مبدا این نظریه به کارهای اولیست گالویس برمیگردد.اوهمچنین در کارهای قبلی خود به طور محسوس از جایگشت استفاده کرده بود.
گروهها در خیلی از ساختارهای جبری از قبیل میدانها و فضای برداری دیده میشوند و ابزار مهمی برای مطالعه تقارن است. به همین دلیل است که نظریه گروهها به عنوان یکی از مهترین مباحث در ریاضیات مدرن است.
بدون تردید یکی از جذاب ترین ویژگیهای ریاضیات جدید تداخلی است
که بین شاخه های مختلف ریاضیات پیش می آید. برای مثال اگر جبر، آنالیز، توپولوژی و با منطق ریاضی را مطالعه کنیم، مشاهده کنیم که ایده های خاصی در تمام این شاخه ها مطرح شوند. مفهوم گروه یکی از همین ایده هاست که همه جا ظاهر می شود. بعلاوه در رشته های دیگری از علوم، مانند شیمی، مکانیک کوانتوم و فیزیک ذرات بنیادی، که در آنها ریاضیات به عنوان ابزار به کار می رود، گروهها اهمیت دارند.
تعریف
فرض کنید که
-
عبارتست از یک مجموعه و * یک عمل دوتایی G است،
-
عمل * شرکت پذیری است،
-
عضو خنثی : عضوی مانند e در G وجود دارد به طوریکه به ازای هر x درG داریم: x*e=e*x=x
-
عضو معکوس : به ازای هر x عضو درG عضوی مانند y در G وجود دارد به طوریکه : x*y=y*x=e
در اینصورت G همراه با عمل دوتایی * گروه نامیده می شود و آنرا با (G, * ) نمایش می دهیم.
توجه کنید که از شرط سوم نتیجه میگیریم که G غیرتهی است. عضو e در G عضو همانی نام دارد (دیری نخواهد پائید که نشان خواهیم داد فقط یک عضو با چنین خاصیتی وجود دارد و در نتیجه خواهیم توانست آنرا عضو همانی بنامیم). عضو y در شرط چهارم معکوس x نام دارد؛ خواهیم دید که هر عضوی مانند x فقط یک معکوس دارد، و از اینرو می توانیم آنرا معکوس x بنامیم. در اینجا شایسته است بر این واقعیت تاکید کنیم که عضو منحصر بفرد همانی e معادلات x*e=e*x=x را به ازای هر x در G ارضا می کند. حال آنکه Y در شرط چهارم به x بستگی دارد. خواهیم دید که دو عضو متمایز G هیچوقت نمی توانند معکوس های برابری داشته باشند و در نتیجه اعضای متفاوت x, معکوس های متفاوتی همچون y خواهند داشت.
همچنین مناسب است تاکید کنیم فرض ما این نیست که * یک عمل جابجائی است. گروههایی که عمل آنها جابجائی است گروههای آبلی نام دارند. این نامگذاری به افتخار ریاضیدان نروژی هنریک آبل (1829 ـ 1802) صورت گرفته است.
قبل از اینکه خواص عمومی گروهها را بررسی کنیم تعدادی مثال را مطرح می کنیم تا نتوانیم کلیت این مفهوم را در ذهن خواننده روشن کنیم. البته از لحاظ تاریخی بعضی از مثال ها قبل از اینکه گروه به صورت مجرد تعریف شود وجود داشته اند؛ مفهوم مجرد گروه زمانی شکل گرفت که مردم متوجه شدند بسیاری از موضوعاتی که مطالعه می کردند دارای مشخصه های ساختاری مشترک هستند و این فکر در آنها قوت گرفت که شاید بتوان با مطالعه مجرد این ویژگیهای مشترک (نه هر کدام بصورت تک تک و جداگانه) به نوعی صرفه جوئی در وقت و دست یافت. در تحلیل پیشرفتهای این موضوع ای تی بل یادآور شده است که هرزمان گروهها خود را ظاهر می سازند و یا می توان آنها را معرفی کرد، سادگی و وضوح از لابلای دریختگی ها درخشش می یابد.
[ شنبه 87/2/7 ] [ 4:32 عصر ] [ مهندسی مکانیک(امین احمدی) ]
سلام سایت www.3RF2008.com افتتاح شد
مطالعه روی زوایا و روابط موجود میان زوایااشکال مسطح و سه بعدی مثلثات نامیده میشود.توابع مثلثاتی از قبیل سینوس و کسینوس توابعی هستند که بوسیله روابط هندسی تعریف میشوند.
تاریخچه
اولین کسانی که از مثلثات استفاده میکردند یونانیان بودند.در یونان قدیم از مثلثات برای تعیین طول مدت روز یا طول سال (با مشخص کردن موقعیت ستارگان در آسمان)استفاده میشد.بعدها ریاضیدانان و منجمان هندی نیز پیشرفتهایی در مثلثات بدست آوردندولی پیشرفت این علم مدیون دانشمندان مسلمان است .مسلمانان اصلی ترین نقش را در پیشرفت این علم ایفا کردند و سپس این اندوخته ها را در قرون وسطی به اروپاییان منتقل کردند.اروپاییان نیز دانش فراوان مسلمانان در مثلثات استفاده کردندو این علم را توسعه داده و به شکل امروزی در آوردند.کاربردها
علم مثلثات در نجوم کاربرد فراوانی دارد و ازآن برای اندازه گیری فواصل بین ستارگان استفاده میشود. همچنین در طراحی سیستم های ماهواره ای از مثلثات استفاده فراوانی میشود.در دریانوردی نیز از مثلثات برای تشخیص جهت های جغرافیایی کمک گرفته میشود.امروزه از مثلثات در شاخه های مختلف فیزیک ماننداپتیک،اکوستیک،در آنالیز بازار مالی،الکترونیک،معماری، اقیانوس شناسی،مکانیک،بلور شناسی،ژئودزی،عمران و اقتصاداستفاده فراوانی میشود.تابع مثلثاتی
مثلثات مطالعه اندازه گیری زاویه است. اما این سخن به معنی اندازه گیری مقدماتی زاویه در هندسه نیست که در آن مقدار زاویه مورد نظر هر یک نقاله خوانده می شود بلکه محاسبه با توابع خاصی است که بستگی به زوایا دارند و به علت کابردشان در مثلثات، توابع مثلثاتی نامیده می شوند.
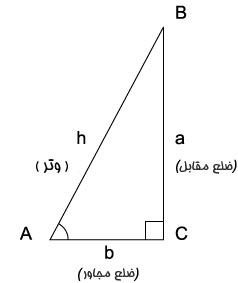 |
تعریف روی مثلث قائم الزاویه
برای تعریف توابع مثلثاتی از یک مثلث قائم الزاویه استفاده می کنیم به عنوان مثال می خواهیم این توابع را برای زاویه A در شکل روبرو تعریف کنیم
ما برای استفاده از این مثلث نامگذاری زیر را انجام می دهیم.
وتر ضلعی است که روبروی زاویه قائم قرار دار که بلندترین ضلع مثلث نیز می باشد و آن را با h نشان داده شده است.
ضلع مقابل زاویه A که آن را با a نشان می دهیم.
ضلع مجاور زاویه قائمه که درشکل با b نشان داده شده است.
حال توابع مثلثاتی را برای زاویه A روی مثلث ABC تعریف می کنیم.
-
sin: نسبت ضلع مقابل به وتر را سینوس می گویند یعنی:
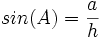
-
cos: نسبت ضلع مجاور به وتر را گویند یعنی داریم:
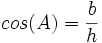
-
tangent: نسبت ضلع مقابل زاویه به ضلع مجاور را گویند.
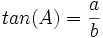
-
cosecant: نسبت وتر به ضلع مقابل زاویه را گویند.
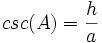
-
secant: نسبت وتر به ضلع مجاور است
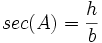
-
cotangent: نسبت ضلع مجاور به ضلع مقابل را گویند.
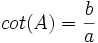
تعریف روی دایره واحد
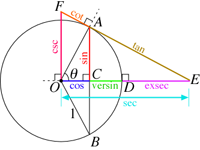 |
در یک صفحه دستگاه مختصات دکارتی، زاویه می تواند هر چهار ربع را طی کند، و مقدار آن می تواند به حسب درجه، گراد رادیان اندازه گیری شود.
ضلع متروک این زاویه، دایره با شعاع و مرکز در مبدا، دایره موسوم به دایره واحد یا یک را در نقطه قطع می کند.
زاویه در تقاطع محور ها با دایره، مقدار صفر را اختیار می کند این زاویه، طی یک دوران کامل ضلع متحرکش حول مبدا از صفحه شروع و پس از رسیدن به مکان اولیه، دارای زاویه 360 درجه می باشد.
روابط مثلثاتی که برای زوایای مختلف برقرار است. برای زوایای بزرگتر از 360 نیز، بر قرار می باشد. مثلا برای دو تابع سینوس و کسینوس خواهیم داشت:
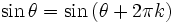
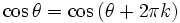
سری فوریه برای بررسی حرکات تناوبی در آکوستیک یا صوت شناسی،الکترودینامیک ،اپتیک یا نور شناسی، ترمودینامیک و غیره مورد استفاده قرار گرفته است.
در مهندسی الکتریک مسائلی چون رفتار بسامدی ،عناصر سوئیچینگ ،یا انتقال ضربه ها را میتوان به کمک سری فوریه حل کرد.
پیش بینی جزرومد در دریانوردی دارای اهمیت فراوانی است.از آنجا که اینها پدیده هایی تناوبی هستند از سری فوریه استفاده میشود و در تمام بندرهای مهم،وسائل مکانیکی چون پیش بینی کننده های جزر و مد ساخته میشود.امروزه کمتر شاخهای از فیزیک،ریاضیات، یا صنعت و فن وجود دارد که در آن از سریهای فوریه استفاده نشود.
تعریف
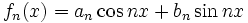
با ضرایب ثابت
 و
و  است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول
است سری مثلثاتی نامیده میشود. اگر این سری در بازهای از طول  همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی
همگرا باشد،آنگاه از آنجا که توابع مثلثاتی تناوبی اند، به ازای جمیع مقادیر x همگراست و تابع تناوبی  ی را نشان میدهد.
ی را نشان میدهد. این تابع لزوما پیوسته نیست، و در واقع اغلب بین آنچه که توسط فرمول های مختلف داده شده است گسستگی هایی دارد.
از طرف دیگر،اگر این سری به طور یکنواخت همگرا باشد،آنگاه مجموع آن،
 ،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب
،پیوسته است. در این حالت میتوان ارتباطی بین ضرایب  و
و  و تابع مجموع
و تابع مجموع  به دست آورد.ضرب سری
به دست آورد.ضرب سری 
در عاملهای کراندار
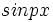 یا
یا 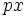 که در آنها p عددی صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان
که در آنها p عددی صحیح و نامنفی است اختلالی در همگرایی یکنواخت آن به وجود نمی آورد،بنابراین میتوان 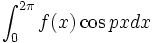 و
و 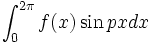
را با استفاده از انتگرالگیری جمله به جمله سری
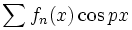 یا
یا 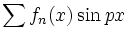 محاسبه کرد
محاسبه کرد این انتگرالگیری ها شامل انتگرال های روی بازه
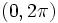 توابع
توابع 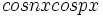 و
و 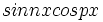 و
و 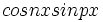 و
و 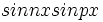 اند.
اند. [ شنبه 87/2/7 ] [ 4:29 عصر ] [ مهندسی مکانیک(امین احمدی) ]
 |
سلام سایت www.3RF2008.com افتتاح شد
اثبات
فرض کنیم O مرکز دایره باشد در آن موقع OA=OB=OCبه این ترتیب OAB و OBC مثلث متساوی الساقین خواهند بود.در نتیجه زوایای OCB=OBC و BAO=ABO.
فرض کنیم Y=BAO و X=OBC ، چون جمع زوایای داخلی مثلث برابر 180 درجه است پس
| 2Y+Z=180 | 2X+Q=180 |
همچنین میدانیم Z+Q=180 .حال اگر دو رابطه اول را با هم جمع و رابطه سوم را از آنها کم نماییم خواهیم داشت:
| 2Y+Z+2X+Q-(Z+Q)=180 |
پس خواهیم داشت:
| Z+Q=90 |
تاریخچه
تالس اولین کسی نبود که این قضیه را کشف کرد قبل از او مصریان و بابلیان این قضیه را میدانستند ولی آنها نتوانسته بودند اثباتی برای آن بیان کنند. چون این قضیه اولین بار توسط تالس به اثبات رسید به نام او نیز معروف شد.البته تالس با استفاده از تعریف مثلث متساوی الساقین و نیز علم به این موضوع که جمع زوایای یک مثلث، 180 درجه است ،این قضیه را اثبات کرد.ویژگیهای هندسی مثلث
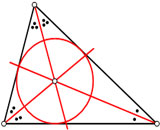
با دانستن خصوصیات بعضی از خطوط مانند ارتفاع یا عمود منصف و یا میانه میتوانیم به نتایج جالبی در مورد دست پیدا کنیم. برخی از این نتایج را بیان میکنیم:
اگر بر سه ضلع مثلث خطوطی را عمود میکنیم به طوریکه این خطوط اضلاع را نصف نمایند.(در واقع عمود منصف اضلاع را رسم میکنیم)در این صورت محل برخورد این سه خط، مرکز دایره ای خواهد بود که مثلث را احاطه میکند . به این دایره، دایره محاطی گویند.این دایره طوری رسم میشود که از سه راس مثلث عبور کند.
طبق قضیه فیثاغورث اگر مرکز دایره محاطی روی یکی از اضلاع قرار گیرد آنگاه زاویه مقابل آن ضلع قائم خواهد بود.به عبارتی دیگر مثلث ما قائم الزاویه خواهد بود. اگر مرکز دایره درون مثلث باشد ،مثلث ما یک مثلث حاده خواهد بود و اگر بیرون مثلث باشد، مثلث از نوع منفرجه خواهد بود.
ارتفاع مثلث خط راستی است که از یک راس مثلث عبور کرده و بر ضلع مقابل آن راس عمود میشود.ضلعی را که ارتفاع بر آن عمود است را قاعده مثلث گویند.طول ارتفاع ، فاصله بین راس و قاعده نظیر ارتفاع است.اگر سه ارتفاع مثلث را رسم کنیم این سه ارتفاع همدیگر را در داخل مثلث قطع میکنند مگر در حالتی که مثلث ،منفرجه باشد.
 |
|
مرکز دایره محیطی است. |
نیمساز یک زاویه از مثلث خط راستی است که از یک راس مثلث گذشته و آن زاویه را به دو قسمت مساوی تقسیم کند.
اگر نیمسازهای سه زاویه مثلث را رسم کنیم این خطوط در نقطه ای درون مثلث همدیگر را قطع خواهند کرد.این نقطه مرکز دایره محیطی مثلث خواهد بود.این دایره درون مثلث قرار دارد به طوریکه اضلاع مثلث، خطوطی مماس بر دایره هستند.
میانه یک مثلث خط راستی است که از راس مثلث گذشته و ضلع مقابل آن را به دو قسمت مساوی تقسیم میکند. سه میانه مثلث یکدیگر را در نقطه ای به نام مرکز مثلث قطع میکنند البته این نقطه مرکز ثقل مثلث نیز میباشدهمچنین این نقطه هر میانه مثلث را به نسبت 1 به 2 تقسیم میکند به طوریکه فاصله میان راس مثلث تا این نقطه دو برابر فاصله این نقطه تا نقطه میانی ضلع مقابل راس است.
دایره های محاطی داخلی و خارجی یک مثلث
 |
|
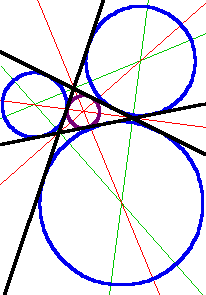
با دایره داخلی (بنفش)، دوایر خارجی (آبی)، نیمسازهای زوایای داخلی (قرمز) و نیمسازهای زوایای خارجی (سبز) |
دایره های محاطی داخلی و خارجی یک مثلث
در هندسه، دایره محاطی داخلی یک مثلث بزرگترین دایرهای است که آن مثلث میتواند در بر بگیرد؛ این دایره سه ضلع آنرا لمس مینماید ( بر آنها مماس میباشد). مرکز دایره محاطی مرکز داخلی مثلث نامیده میشود. یک دایره محاطی خارجی مثلث، یک دایره در خارج مثلث است که بر یکی از اضلاع مثلث و امتداد دو ضلع دیگر مماس باشد. هر مثلث دارای سه دایره محاطی خارجی متمایز، که هر کدام بر یکی از اضلاع مثلث مماس میباشد.
مرکز دایره محاطی داخلی بر روی تقاطع نیمسازهای زوایای داخلی قرار دارد. مرکز یک دایره محاطی خارجی بر روی تقاطع نیمساز یک زاویه داخلی و نیمسازهای خارجی دو زاویه دیگر قرار دارد. از این رو، استنباط میگردد که مرکز دایره محاطی داخلی و سه مرکز دایره های محاطی خارجی یک سیستم چهارمرکزی (orthocentric) را تشکیل میدهند.
شعاع این دوایر ارتباط نزدیکی با سطح یک مثلث دارد. اگر S سطح مثلث و اضلاع آن b ،a و c باشند،
شعاع دایره داخلی ( که "شعاع داخلی" نیز گفته میشود) برابر است با: (S/(2(a+b+c).
شعاع دایره خارجی در سمت a برابر است با: (S/(2(-a+b+c)،
برای دایره در سمت b برابر است با: (S/(2(a-b+c)
و برای دایره در سمت c برابر است با: (S/(2(a+b-c).
از این روابط درمیابیم که دوایر خارجی از دایره داخلی بزرگتراند و بزرگترین دایره خارجی، دایره ای است که به بزرگترین ضلع چسبیده است.
| Triangle with incircle, contact triangle and Gergonne point |
|
مثلث تماس (قرمز)، نقطه جرگونه (سبز) |
دایره نه نقطه ای مثلث بر سه دایره خارجی و همچنین دایره داخلی مماس میباشد. نقطه فورباخ(Feuerbach) روی دایره داخلی قرار دارد.
با علامت گذاری رئوس مثلث با B، A و C و سه نقطه تماس دایره داخلی و مثلث با TB، TA و TC (که TA روبروی A قرار داشته و به همین ترتیب بقیه)، مثلث TATBTC مثلث تماس ABC نامیده میشود. دایره داخلی ABC یک دایره محیطی بر TATBTC میباشد. سه خط BTB ، ATA و CTC در یک نقطه
 |
|
|
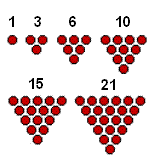
1، 3، 6، 10، 15، 21 و ... بنظر شما این اعداد چه ویژگی مشترکی دارند؟ اگر دست به قلم نشویم و شکل نکشیم و آزمایش نکنیم، فهمیدن ارتباط میان آنها کمی دشوار است. به این شکل دقت کنید مشکل شما حل خواهد شد. به اعداد موجود در این سری، اعداد مثلثی می گوییم.
1 = 1
3= 1+2
6= 1+2+3
10= 1+2+3+4
15= 1+2+3+4+5
21= 1+2+3+4+5+6
. . .
اما شکل اول یک ایده جدید به ما می دهد که می توانیم این اعداد را همانند پاراگراف بالا نیز تفسیر کنیم.
به بیان دیگر می توان گفت که هرعدد مثلثی تشکیل شده است از حاصل جمع یکسری از اعداد متوالی طبیعی. به این معنی که اولین عدد مثلثی مساوی است با مجموع یک عدد از اعداد طبیعی، دومین معادل است با مجموع دو عدد از اعداد طبیعی، سومین معادل است با مجموع سه عدد از اعداد طبیعی و ... و بالاخره n امین عدد مثلثی معادل است با مجموع n عدد از اعداد طبیعی که اگر ریاضیات دبیرستان را هنوز فراموش نکرده باشید بخاطر خواهید آورد که مقدار این عدد معادل n(n+1)/2 خواهد بود. (یک تصاعد حسابی ساده)
 |
|
|
مجموع دو عدد مثلثی متوالی اگر هر دو عدد پشت سرهم در سری اعداد مثلثی را با هم جمع کنیم حاصل جمع یک عدد مربع می شود. مثلا" 1+3=4 یا 3+6=9 یا 6+10=16 و ... البته دلیل آن ساده است به شکل دوم توجه کنید و ببینید که چگونه دو مثلث قرمز و سبز روی هم تشکیل یک مربع را می دهند. (سعی کنید با استدلال ریاضی هم این موضوع را ثابت کنید، ساده است از همان رابطه بالا استفاده کنید.)
مطلب اخیر اغلب بصورت قضیه مربع هر عدد طبیعی برابر است با مجموع دو عدد مثلثی متوالی نیز مطرح می شود.
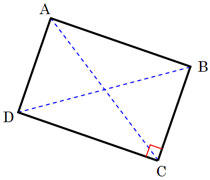 |
مستطیل
در هندسه، مستطیل، یک جهارضلعی با زوایای قائم است.همچنین در یک مستطیل اضلاع روبرو دارای طولهای مساوی هستند.یک مربع نوع خاصی از مستطیل است که دارای چهار ضلع مساوی می باشد.
یک مربع ،میتواند هم یک مستطیل و هم یک متوازی الاضلاع باشد. ولی عکس این مطلب برقرار نیست.
در یک مستطیل یک جفت از اضلاع را که طویل ترند را طول مستطیل و جفت دیگر اضلاع را که کوتاهترند را عرض مستطیل نامند.
مساحت یک مستطیل برابر از ضرب اندازه طول مستطیل در عرض آن حاصل میشود.هر مستطیل دارای دو قطر است که اندازه این قطرها از فرمول زیر محاسبه میشود:(a طول مستطیل وb عرض آن است) 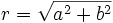
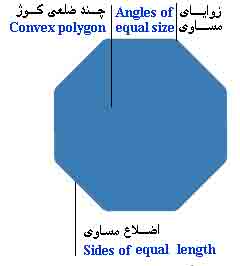
چند ضلعی
مثلث، مربع، و پنج ضلعی نمونه ای از چند ضلعی ها هستند. در یک چند ضلعی منتظم، ضلعها طول مساوی دارند و اندازه زوایای داخلی نیز مساوی است.هر قدر تعداد اضلاع یک چند ضلعی منتظم بیشتر باشد، بیشتر شبیه دایره خواهد بود. دو نوع چند ضلعی وجود دارد: کوژ و کاو.
در چند ضلعی کوژ همه گوشه ها رو به بیرونند.در چند ضلعی کاو یک یا چند گوشه رو به داخلند.
 |
 |
 |
 |
 |
 |
[ پنج شنبه 87/2/5 ] [ 5:46 عصر ] [ مهندسی مکانیک(امین احمدی) ]

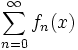 که جمله عمومی آن
که جمله عمومی آن 